Kinematic Bicycle Model em Python

por Heitor Tonet
em Códigos Python
on 3 de junho de 2024

Hoje vamos aprender a desenvolver o Kinematic Bicycle Model (Modelo Cinemático da Bicicleta), um modelo utilizado em carros autônomos, trata-se de um modelo clássico que se sai surpreendentemente bem na captura do movimento do veículo em condições normais de condução, vamos entender um pouco da teoria e depois vamos implementar na prática.

O Kinematic Bicycle Model tem sido usado há muito tempo como um modelo adequado orientado ao controle para representar veículos devido à sua simplicidade e aderência às restrições não holonômicas de um carro. O modelo que será desenvolvido é chamado de modelo de direção da roda dianteira, pois a orientação da roda dianteira pode ser controlada em relação à direção do veículo. Vamos assumir que o veículo opera em um plano 2D denotado pelo referencial FI. No modelo proposto, a roda dianteira representa as rodas dianteiras direita e esquerda do carro, e a roda traseira representa as rodas traseiras direita e esquerda.

Para analisar a cinemática do modelo, devemos selecionar um ponto de referência X e Y no veículo, que pode ser colocado no centro do eixo traseiro, no centro do eixo dianteiro, ou no centro de gravidade ou cg. A seleção do ponto de referência altera as equações matemáticas resultantes, que por sua vez, altera os designs do controlador que será usado.

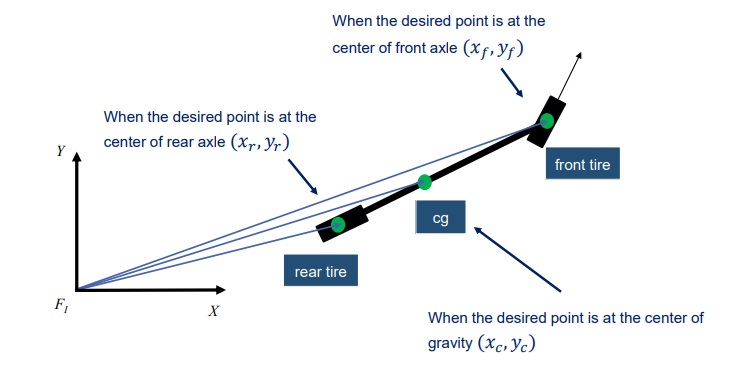
Vamos começar com o modelo do ponto de referência do eixo traseiro. Denotaremos a localização do ponto de referência do eixo traseiro como xr, yr e o rumo da bicicleta como Theta. Usaremos L para o comprimento da bicicleta, medido entre os dois eixos das rodas.

Agora, vamos definir um ângulo de direção para a roda dianteira, que será chamado de Delta e medido em relação à direção de avanço da bicicleta. A velocidade será denotada por v e aponta na mesma direção da cada roda, esta é uma suposição conhecida como condição de não deslizamento, que não permite que a roda se mova lateralmente ou deslizar longitudinalmente.

Devido à condição de não deslizamento, temos Ômega que é a taxa de rotação da bicicleta, que é igual à velocidade sobre o centro instantâneo de rotação, raio R. A partir dos triângulos semelhantes formados por L e R e v e Delta, podemos perceber que a tan de Delta é igual à distância entre os eixos L sobre o raio de giro instantâneo R.

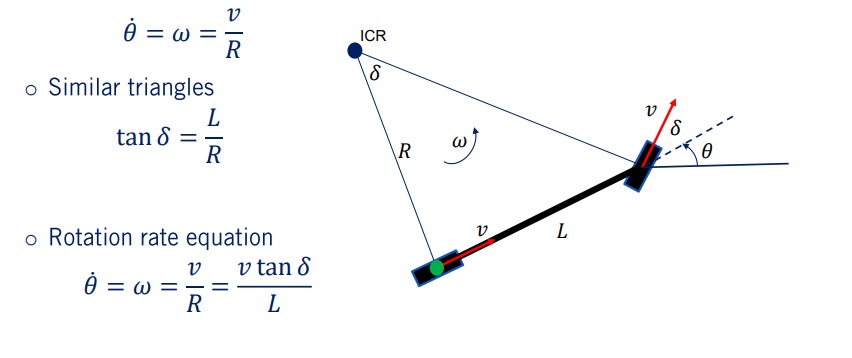
Combinando as duas equações, podemos encontrar a relação entre a taxa de rotação do veículo Ômega e o Delta do ângulo de direção, já que Ômega é igual a v tan Delta sobre L. Podemos agora formar o modelo cinemático completo da bicicleta para o ponto de referência do eixo traseiro. Com base nesta configuração do modelo, os componentes de velocidade do ponto de referência na direção x e y são iguais à velocidade v multiplicado por cos de Theta e sen de Theta respectivamente.

Estas duas equações são combinadas com a equação da taxa de rotação derivada anteriormente para formar o modelo da bicicleta com eixo traseiro.

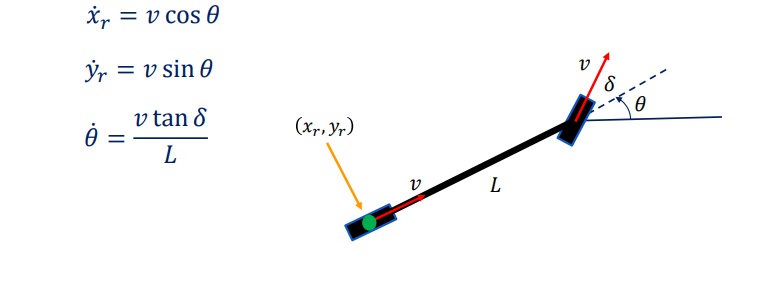
O modelo pode ser reformulado quando o centro do eixo dianteiro é tomado como ponto de referência x e y. Desta vez, a velocidade aponta na direção da roda dianteira, que é definida pelo soma de Delta e Theta.

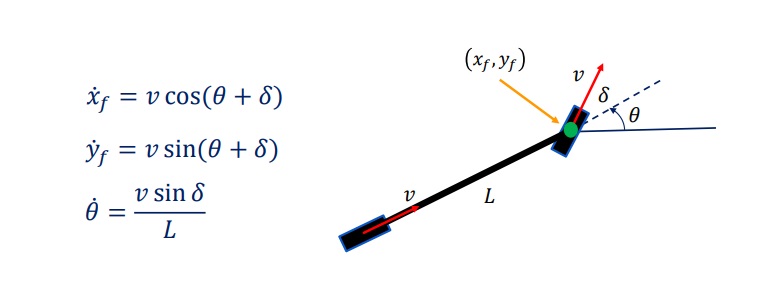
Trabalhando através da derivação nos leva ao seguinte modelo cinemático para o veículo. No último cenário é quando o ponto desejado é colocado no centro de gravidade ou centro de massa conforme mostrado na figura abaixo.

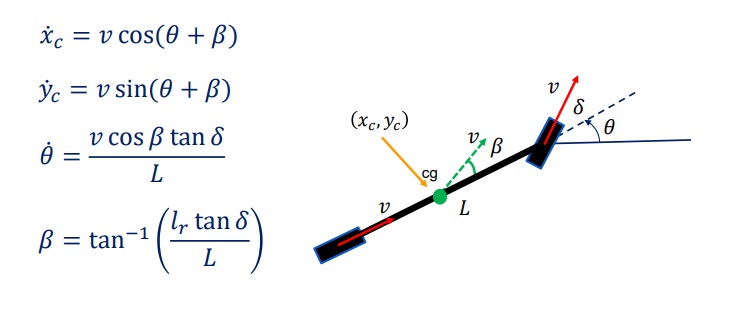
Devido as restrições de não deslizamento que aplicamos às rodas dianteiras e traseiras, a direção do movimento no centro de gravidade é ligeiramente diferente da direção da velocidade de avanço em qualquer roda e da direção da bicicleta. Essa diferença é chamada de ângulo de deslizamento lateral, que iremos chamar de Beta, é medido como a diferença angular entre a velocidade no centro de gravidade e a direção da bicicleta.

Por último, devido à condição de não deslizamento, podemos calcular o ângulo de deslizamento a partir da geometria do nosso modelo de bicicleta. Dado LR, à distância da roda traseira ao centro de gravidade, o ângulo de deslizamento Beta é igual à razão de LR sobre L multiplicado pela tan Delta.

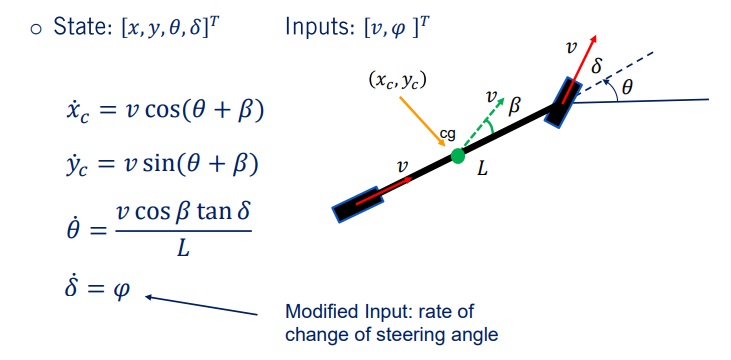
Normalmente não é possível alterar instantaneamente o ângulo de direção de um veículo de um extremo para o outro do seu alcance, como atualmente é possível com o nosso modelo cinemático. Como Delta é uma entrada que seria selecionada por um controlador, não há restrição sobre a rapidez com que ela pode mudar, o que é um tanto irrealista. Em vez disso, os modelos cinemáticos podem ser formulados com quatro estados: x, y, Theta e Delta do ângulo de direção.

Se assumirmos que só podemos controlar a taxa de mudança do ângulo de direção Phi, podemos simplesmente estender nosso modelo para incluir Delta como um estado e usar a taxa de direção Phi como nossa entrada modificada. O Kinematic Bicycle Model agora está completo.

Nosso modelo cinemático de bicicleta toma como entradas a velocidade e a taxa de direção Phi. O estado do sistema, incluindo as posições XC e YC. A orientação Theta e o ângulo de direção Delta, evoluem de acordo com as equações cinemáticas do modelo, que satisfazem a condição de não deslizamento. Agora podemos utilizar este modelo para projetar controladores de direção cinemática.

Depois de uma breve explicação sobre a teoria, vamos para a implementação em Python. O projeto consiste em implementar o modelo cinemático, o modelo aceita entradas de velocidade e taxas de direção e percorre as equações cinemáticas, em seguida vamos fornecer um conjunto de entradas para que a bicicleta seja conduzida em um trajeto em forma de 8.

O kinematic Bicycle Model é guiado pela seguinte conjunto de equações:

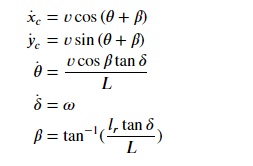
As entradas serão:

𝑣 – velocidade da bicicleta;

𝜔 – taxa do ângulo de direção;

A entrada também pode ser diretamente o ângulo de direção 𝛿 e não a sua taxa no caso simplificado. O modelo em Python permite ambas as implementações, além das classes Python que usaremos que nos permite armazenar as variáveis de estado e criar funções para implementar o Kinematic Bicycle Model.

A bicicleta vai começar com uma condição inicial 0, uma taxa de giro máxima de 1,22 rad/s, uma distância entre os eixos de 2m e um comprimento de 1,2m até o centro de massa à partir do eixo traseiro.

Vamos começar importando as bibliotecas:

BicycleSolution – para o Bicycle Model;

Numpy – para realizar operações em arrays multidimensionais;

Matplotlib – para visualizações gráficas.

Um tempo de amostra é necessário para a integração numérica ao propagar a cinemática ao longo do tempo, isso está definido para 10 milissegundos t_sample = 10e-3. Também temos uma função de redefinição que define todas as variáveis de estado de volta para zero.

Com este tempo de amostragem, vamos implementar o modelo cinemático usando a função definida na próxima célula. a função deve tomar a velocidade + taxa angular como entradas e atualizar as variáveis de estado, além da taxa máxima de rotação da bicicleta.

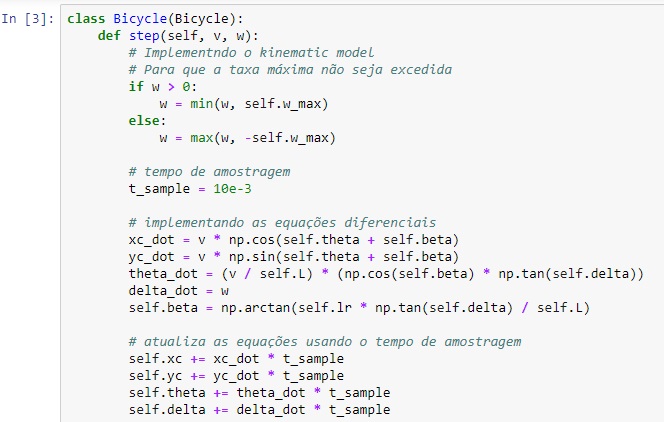
Com o modelo configurado podemos fornecer informações e produzir trajetos.

Tomamos como exemplo um modelo que percorre um círculo de raio 10m em 20 segundos. Usando a relação entre o raio de curvatura e o ângulo de direção, o ângulo de direção desejado pode ser calculado:

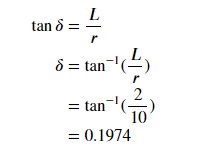
Se o ângulo de direção for definido diretamente para 0,1974 usando um modelo de bicicleta simplificado, a bicicleta se moverá em círculo sem exigir qualquer comando de direção adicional.

A velocidade desejada pode ser calculada à partir da circunferência do círculo:

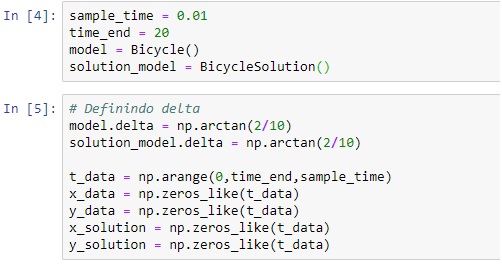
Vamos implementar um loop para percorrer as equações do modelo.

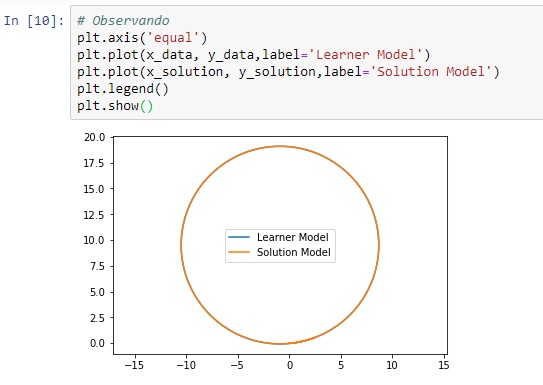
Agora vamos mostrar a trajetória do modelo executado. Percebemos que o gráfico mostra o círculo desejado com raio de 10m.

Exemplo com caminho quadrado.

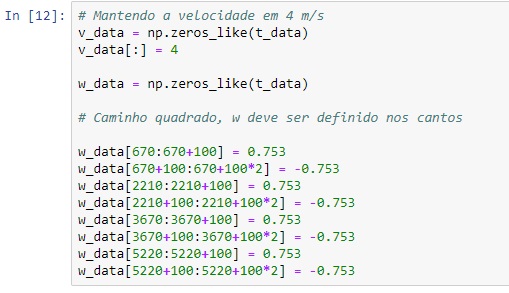
Visualizando a rota que foi traçada corretamente.

Agora vamos para o real objetivo do projeto, que é fazer com que a bicicleta percorra um trajeto em forma de 8. Na figura abaixo temos 2 círculos, ambos com raio = 8m e o caminho deve ser concluído em 30 segundos. O caminho se inicia na parte inferior do círculo esquerdo como mostrado na imagem.