Como Funciona a Aprendizagem Por Reforço?

O Aprendizado por Reforço ou Reinforcement Learning (RL) é um subconjunto crescente do machine learning e uma das fronteiras mais importantes da Inteligência Artificial, uma vez que ganhou grande popularidade nos últimos anos com muitas aplicações bem sucedidas no mundo real e na robótica, jogos e muitos outros campos. Denota um conjunto de algoritmos que lidam com a tomada de decisões sequenciais e têm a capacidade de tomar decisões inteligentes dependendo do ambiente local.

Um algoritmo RL pode ser descrito como um modelo que indica a um agente no qual o conjunto de ações ele deve realizar dentro de um ambiente fechado para maximizar uma recompensa global predefinida. De modo geral, o agente tenta diferentes conjuntos de ações, avaliando o retorno total obtido. Depois de muitas tentativas, o algoritmo aprende quais ações dão maior recompensa e estabelece um padrão de comportamento. Graças a isso, é capaz de informar ao agente quais ações tomar em cada condição.

O objetivo do RL é capturar estruturas mais complexas e usar algoritmos mais adaptáveis ​​​​do que o aprendizado de máquina clássico. Na verdade, os algoritmos de RL são mais dinâmicos em seu comportamento em comparação com os algoritmos de aprendizado de máquina clássico.

Vejamos alguns exemplos de aplicações baseadas em RL:

Robótica – pode ser usada para problemas de controle de alta dimensão e para diversas aplicações industriais;

Mineração de texto – juntamente com um modelo de geração de texto, pode ser usada para desenvolver um sistema capaz de produzir resumos altamente legíveis de textos longos;

Execução comercial – as principais empresas do setor financeiro usam algoritmos RL para melhorar sua estratégia comercial;

Healthcare – é útil para dosagem de medicamentos e para otimização do tratamento de pessoas que sofrem de problemas clínicos crônicos, etc;

Games – RL é famoso por ser o principal algoritmo usado para resolver diversos jogos e obter desempenhos sobre-humanos.

Atores

Os algoritmos RL são baseados no Processo de Decisão de Markov (MDP) que é um processo de decisão estocástico especial de controle de tempo para tomada de decisão. Os principais atores de um algoritmo RL são:

Agente – entidade que realiza ações em um ambiente para otimizar uma recompensa de longo prazo;

Ambiente – o cenário em que o agente toma decisões;

Conjunto de estados (S) – conjunto de todos os estados ‘s’ possíveis do ambiente, onde o estado descreve a situação atual do ambiente;

Conjunto de ações (A) – conjunto de todas as ações possíveis que podem ser realizadas pelo agente;

Modelo de transição de estado P (s_0|s , a) – descreve a probabilidade do estado do ambiente mudar em s_0 quando o agente executa a ação a no estado s , para cada estado s , s_0 e ação a;

Recompensa (r = R(s , a)) – uma função que indica a recompensa imediata e real avaliada pela ação a no estado s;

Episódio (rollout) – é uma sequência de estados st e ações em for t que varia de 0 até um valor final L (que é chamado de horizonte e pode eventualmente ser infinito); o agente inicia em um determinado estado do seu ambiente; a cada passo de tempo t o agente observa o estado atual s_t ∈ S e consequentemente executa uma ação a_t ∈ A ; o estado evolui para um novo estado s_(t+1) , que depende apenas do estado s_t e da ação a_t , conforme o modelo de transição de estado; o agente obtém uma recompensa r_t ; então o agente observa o novo estado s_(t+1)∈ S e o loop é reiniciado;

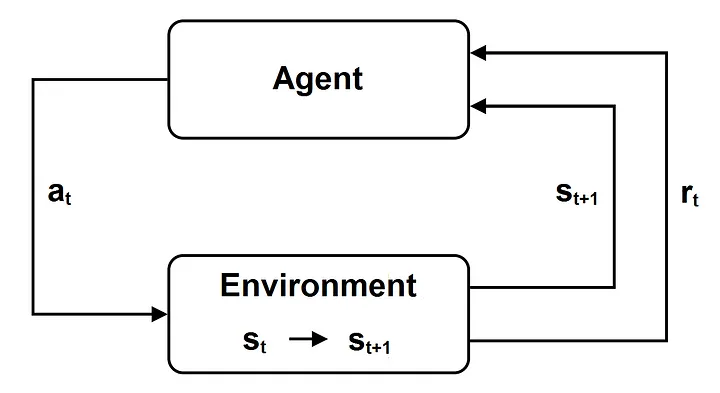
Função política – uma política pode ser determinística ( π(s) ) ou estocástica ( (a|s) ); uma política determinística π(s) indica a ação a ser realizada pelo agente quando o ambiente está no estado s ( a =π(s) ); uma política estocástica π (a|s) é uma função que descreve a probabilidade de que a ação a seja executada pelo agente quando o ambiente está no estado s. Uma vez especificada a política, o novo estado depende apenas da política e do modelo de transação estatal;

Retorno G_t – a recompensa total de longo prazo com desconto obtida ao final do episódio, de acordo com a recompensa imediata do timestep atual e de todos os timesteps seguintes, e do fator de desconto γ < 1:

Função de valor V(s) – o retorno esperado de longo prazo no final do episódio, começando no estado s no intervalo de tempo atual t:

Função Q-Value ou Action-Value Q(s , a) – o retorno esperado de longo prazo no final do episódio, partindo do estado s no timestep atual e executando a ação a;

Equação de Bellman – o núcleo teórico na maioria dos algoritmos RL de acordo com ele, a função valor atual é igual à recompensa atual mais ela mesma avaliada na próxima etapa e descontada por γ (lembramos que na equação P é o modelo de transição do modelo):

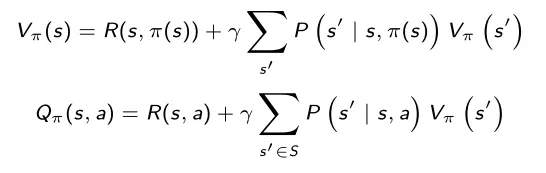
Política Ideal

O máximo da função de valor de ação, à medida que a política muda, é referido como a função de valor de ação ideal Q*(s , a) , e de acordo com a equação de Bellman é dado por:

Então a política ideal π*(s) é dada pela ação que maximiza a função valor da ação:

O problema é que na maioria dos casos reais o modelo de transição de estado e a função de recompensa são desconhecidos, por isso é necessário aprendê-los por amostragem para estimar a função de valor de ação ótima e a melhor política. Por estas razões são utilizados algoritmos RL, a fim de realizar as ações no ambiente, observar e aprender a dinâmica do modelo, estimar a função de valor ideal e a política ótima, e melhorar as recompensas.

Exploration-exploitation

A exploração é o treinamento em novos pontos de dados, enquanto a exploração é o uso dos dados previamente capturados. Se continuarmos buscando a melhor ação em cada iteração, poderemos permanecer parados em um conjunto limitado de estados, sem sermos capazes de explorar todo o ambiente. Para sair deste conjunto sub-ótimo, geralmente é utilizada uma estratégia chamada ϵ-gulosa: quando selecionamos a melhor ação, há uma pequena probabilidade ϵ de que uma ação aleatória seja escolhida.

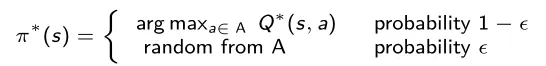
Abordagens

Existem 3 abordagens principais possíveis que podemos usar quando implementamos um algoritmo RL:

Métodos baseados em valor – um algoritmo baseado em valor aproxima a função de valor ideal, ou a função de valor de ação ideal, melhorando continuamente sua estimativa. Normalmente, a função de valor ou a função de valor de ação são inicializadas aleatoriamente e, em seguida, são atualizadas continuamente até convergirem. É garantido que um algoritmo baseado em valor convirja para os valores ideais.

Métodos baseados em políticas – um algoritmo baseado em políticas procura uma política onde a ação executada em cada estado seja ideal para obter a recompensa máxima no futuro. Ele redefine a política a cada passo e calcula a função de valor de acordo com esta nova política até que a política convirja. Um método baseado em políticas também tem garantia de convergência para a política ideal e geralmente leva menos iterações para convergir do que os algoritmos baseados em valores.

Métodos baseados em modelo – um algoritmo baseado em modelo aprende um modelo virtual a partir do ambiente original e o agente aprende como atuar no modelo virtual. Utiliza um número reduzido de interações com o ambiente real durante a fase de aprendizagem, depois constrói um novo modelo baseado nessas interações, utiliza esse modelo para simular os próximos episódios e obter os resultados retornados pelo modelo virtual.

Métodos Baseados em Valor

Aproximação de função de valor

A aproximação da função de valor é um dos métodos mais clássicos baseados em valores. Seu objetivo é estimar a política ideal π*(s) aproximando iterativamente a função de valor de ação ótima Q*(s , a) . Começamos considerando uma função paramétrica de valor de ação Q^(s , a , w) , onde w é um vetor de parâmetros. Inicializamos aleatoriamente o vetor w e iteramos em cada etapa de cada episódio. Para cada iteração, dado o estado s e a ação a , observamos a recompensa R(s , a) e os novos estados s‘. De acordo com a recompensa obtida atualizamos os parâmetros utilizando o gradiente descendente:

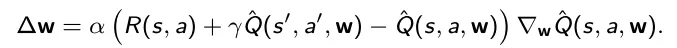
Na equação, α é a taxa de aprendizagem. Pode-se dizer que este processo converge, e a função de valor de ação obtida é a nossa aproximação da função de valor de ação ótima. Na maioria dos casos reais a melhor escolha para a função paramétrica de valor de ação Q^(s , a , w) é uma rede neural, e então o vetor de parâmetros w é dado pelo vetor dos pesos da rede neural.

Algoritmo de aproximação de função de valor:

Deep Q-Network

Uma Deep Q-Network é uma combinação de Deep Learning e RL, pois é um algoritmo de aproximação de função de valor onde a função de valor de ação paramétrica Q^(s, a, w) é uma rede neural profunda, em particular, uma rede neural convolucional . Além disso, uma Deep Q-Network supera o aprendizado instável usando principalmente 2 técnicas:

Rede Alvo – as atualizações do modelo podem ser muito instáveis, pois o alvo real muda cada vez que o modelo é atualizado, então a solução é criar uma rede alvo Q^(s’,a’,w’) , que é uma cópia do modelo de treinamento que é atualizado com menos frequência, por exemplo a cada mil passos (indicamos como w’ os pesos do rede alvo). Em cada atualização do modelo com gradiente descendente, a rede alvo é usada como alvo no lugar do próprio modelo:

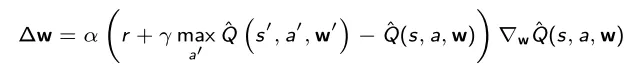
Experience Replay – no algoritmo descrito, várias atualizações consecutivas são realizadas usando dados do mesmo episódio, e isso pode causar overfitting. Para resolver isso, é criado um buffer experience replay que armazena as quatro tuplas ( s , a , r , s’ ) de todos os diferentes episódios, e seleciona aleatoriamente um lote de tuplas cada vez que o modelo é atualizado. Esta solução tem 3 vantagens: reduz o overfitting, aumenta a velocidade de aprendizado com minilotes e reutiliza tuplas anteriores para evitar esquecimentos.

Fitted Q-Iteration

Outro algoritmo popular baseado em valor é o Fitted Q-Iteration. Considere o caso determinístico, no qual temos que os novos estados s’ são determinados unicamente pelo estado s e pela ação a de acordo com alguma função a f , então podemos escrever s’ = f (s , a) . Seja L o horizonte, possivelmente infinito, e lembramos que o horizonte é a duração de todos os episódios. O objetivo deste algoritmo é estimar a função de valor de ação ideal. Pela equação de Bellman, a função de valor de ação ótima Q*(s , a) pode ser vista como a aplicação de um operador H à função de valor de ação Q(s , a):

Considere agora um horizonte temporal N menor ou igual ao horizonte L , e denote por Q_N (s, a) a função de valor de ação em N etapas definidas pela aplicação do operador H recém definido à função de valor de ação Q_(N− 1) (s , a) , com

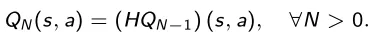
É possível mostrar que esta sequência de funções de valor de ação de N passos Q_N (s , a) converge para a função de valor de ação ótima Q*(s , a) como N → L . Graças a isso, é possível construir um algoritmo para aproximar a função de valor de ação ideal Q*(s , a) iterando em N.

Algoritmo Q-Iteration ajustado:

Métodos Com Policy Gradient

Gradiente de política

Policy Gradient é o método mais clássico baseado em políticas. O objetivo do método Policy Gradient é encontrar o vetor de parâmetros θ que maximiza a função de valor V (s , θ) sob uma política paramétrica π (a|s , θ).

Começamos por considerar uma política paramétrica π (a|s , θ) diferenciável em relação ao vetor de parâmetros θ; em particular neste caso escolhemos uma política estocástica (neste caso o método é denominado Gradiente de Política Estocástica, porém o caso com uma política determinística é muito semelhante).

Inicializamos aleatoriamente o vetor w e iteramos em cada episódio. Para cada timestep t geramos uma sequência de trigêmeos (s , a , r) escolhendo a ação de acordo com a política paramétrica π (a|s , θ). Para cada intervalo de tempo na sequência resultante calculamos a recompensa total de longo prazo com desconto G_t em função das recompensas obtidas:

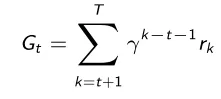
Em seguida, o vetor de parâmetros θ_t é modificado usando um processo de atualização de gradiente

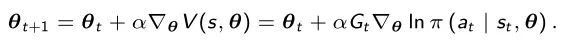
Na equação α > 0 é a taxa de aprendizagem. Pode ser mostrado que este processo converge, e o processo obtido é a nossa política ótima aproximada.

Algoritmo Policy Gradient:

Exemplos de políticas paramétricas

As políticas paramétricas mais utilizadas são a Política Softmax e a Política Gaussiana.

Política Softmax

A Política Softmax consiste em uma função softmax que converte a saída em uma distribuição de probabilidades e é usada principalmente no caso de ações discretas:

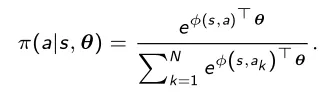
Neste caso a fórmula explícita para a atualização do gradiente é dada por

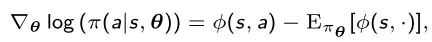
onde φ(s , a) é o vetor de características relacionado ao estado e à ação.

Política Gaussiana

A Política Gaussiana é utilizada no caso de um espaço de ação contínua e é dada pela função Gaussiana

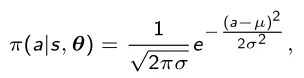
onde µ(s) é dado por φ(s) T θ, φ(s , a) é um vetor de características e σ pode ser fixo ou paramétrico. Também neste caso temos a fórmula explícita para a atualização do gradiente:

Vantagens do Policy Gradient

1 – O método Policy Gradient é um processo mais simples em comparação com métodos baseados em valor;

2 – Permite que a ação seja contínua em relação ao estado;

3 – Geralmente possui melhores propriedades de convergência em relação a outros métodos;

4 – Evita o crescimento do uso de memória e do tempo de computação quando os conjuntos de ações e estados são grandes, pois o objetivo é aprender um conjunto de parâmetros cujo tamanho é muito menor que o do conjunto de estados e do conjunto de ações;

5 – Pode aprender políticas estocásticas;

6 – Permite a utilização do método ϵ-guloso, para que o agente possa ter uma probabilidade ϵ de realizar ações aleatórias.

Desvantagens do Policy Gradient

1 – O método de gradiente de política normalmente converge para um ótimo local em vez de global;

2 – Geralmente tem alta variância (que entretanto pode ser reduzida com algumas técnicas).

Método Ator-Crítico

Outro método popular baseado em políticas é o Ator-Crítico. É diferente do método Policy Gradient porque estima a função de política e de valor e atualiza ambas. No Policy Gradient, o vetor de parâmetros θ é atualizado usando a recompensa de longo prazo G_t , mas essa estimativa geralmente apresenta alta variância. Para resolver esse problema e reduzir as grandes mudanças nos resultados, a ideia do método Ator-Crítico é subtrair da recompensa total com desconto G_t uma linha de base b(s).

O valor obtido δ = Gt – b(s) , que é denominado erro de diferença temporal, é utilizado para atualizar o vetor de parâmetros θ no lugar da recompensa de longo prazo G_t. As linhas de base podem assumir diversas formas, mas a mais utilizada é a estimação da função valor V(s).

Como nos métodos baseados em valor, a função de valor V(s) pode ser aprendida com uma rede neural, cuja saída é a função de valor aproximado V^(s , w) , onde w é o vetor de pesos. Então, em cada iteração, o erro de diferença temporal δ é usado não apenas para ajustar o vetor de parâmetros θ, mas também para atualizar o vetor de pesos w.

Este método é denominado Métodos Ator-Crítico, porque: O Crítico estima a função de valor V(s) e porque o Ator atualiza a distribuição de políticas na direção sugerida pelo Crítico (como nos métodos de gradiente de políticas).

Algoritmo Ator-Crítico:

Método baseado em modelo

Conforme já sublinhado, um método baseado em modelo cria um modelo virtual a partir do ambiente original, e que o agente aprende como atuar no modelo virtual. Um método baseado em modelo começa considerando um modelo paramétrico básico e, em seguida, executa as três etapas a seguir:

1 – Atuação: a política base π_0(a_t|s_t) é utilizada para selecionar as ações a serem executadas no ambiente real, a fim de coletar um conjunto de observações dadas pelos trigêmeos (estado, ação, novo estado);

2 – Aprendizagem do modelo: a partir da experiência coletada, um novo modelo m(s , a) é deduzido a fim de minimizar o erro mínimo quadrático entre o novo estado do modelo e o novo estado real, um algoritmo de aprendizagem supervisionada pode ser usado para treinar um modelo para minimizar o erro mínimo quadrado da trajetória amostrada;

3 – Planejamento: a função de valor e a política são atualizadas de acordo com o novo modelo, para serem utilizadas na seleção das ações a serem executadas no ambiente real na próxima iteração.

Um dos modelos mais utilizados para representar a dinâmica do sistema é o Processo Gaussiano, no qual a predição interpola as observações utilizando a distribuição Gaussiana. Outra possibilidade é utilizar o Modelo de Mistura Gaussiana, que é um modelo probabilístico que assume que todos os pontos de dados são gerados a partir de uma mistura de um número finito de distribuições gaussianas com parâmetros desconhecidos. É uma espécie de generalização do agrupamento k-Means que incorpora informações sobre a estrutura de covariância dos dados, bem como os centros das Gaussianas latentes.

Algoritmo de amostra de método baseado em modelo:

Controle Preditivo de Modelo

O Controle Preditivo Modelo é uma evolução do método que acabamos de descrever. O algoritmo baseado no modelo descrito é vulnerável a desvios, pois pequenos erros se acumulam rapidamente ao longo da trajetória e o espaço de busca é muito grande para que qualquer política básica seja totalmente coberta. Por esta razão a trajetória pode chegar a áreas onde o modelo ainda não foi aprendido. Sem um modelo adequado nessas áreas, é impossível planejar o controle ideal.

Para resolver isso, em vez de aprender o modelo no início, a amostragem e o ajuste do modelo são realizados continuamente durante a trajetória. No entanto, o método anterior executa todas as ações planejadas antes de ajustar novamente o modelo.

No Controle Preditivo de Modelo, toda a trajetória é otimizada, mas apenas a primeira ação é executada, depois o novo trio ( s , a , s’ ) é adicionado às observações e o planejamento é feito novamente, isto permite tomar uma ação corretiva caso o estado atual seja observado novamente. Para um modelo estocástico, isso é particularmente útil.

Ao mudar constantemente o plano, o MPC fica menos vulnerável a problemas no modelo. O novo algoritmo executa 5 etapas, das quais as 3 primeiras são iguais ao algoritmo anterior (atuação, aprendizagem de modelo, planejamento). Então nós temos:

1 – Atuando;

2 – Aprendizagem do modelo;

3 – Planejamento;

4 – Execução: onde a primeira ação planejada é executada e os estados resultantes são observados;

5 – Atualização do conjunto de dados: o novo trio ( s , a , s’ ) é anexado ao conjunto de dados; vá para o passo 3, a cada N vezes vá para o passo 2 (como já visto, isso significa que o planejamento é realizado a cada passo, e que o modelo é ajustado a cada N passos da trajetória).

Vantagens e desvantagens dos métodos baseados em modelo

O RL baseado em modelo tem uma forte vantagem de ser muito eficiente com poucas amostras, uma vez que muitos modelos se comportam linearmente, pelo menos na proximidade local. Uma vez conhecidos o modelo e a função de recompensa, o planejamento dos controles ótimos não requer amostragem adicional. Geralmente a fase de aprendizagem é rápida, pois não há necessidade de esperar que o ambiente responda nem de redefinir o ambiente para algum estado para retomar a aprendizagem.

Por outro lado, se o modelo for impreciso, corremos o risco de aprender algo completamente diferente da realidade. Outro ponto que não vale a pena é que o algoritmo baseado em modelo ainda utiliza métodos livres de modelo tanto para construir o modelo quanto nas fases de planejamento e simulação.

Conclusão

O principal desafio da RL reside na preparação do ambiente de simulação e na escolha da abordagem mais adequada. Esses aspectos são altamente dependentes da tarefa a ser executada e são muito importantes porque muitos problemas do mundo real têm enormes espaços de estado ou ação que devem ser representados de forma eficiente e abrangente.