Falha no Sistema de Pressão de Ar em Caminhões da Scania

Neste projeto de machine learning vamos criar um modelo preditivo para prever com a maior precisão possível falhas no sistema de pressão de ar dos caminhões da Scania, este sistema gera ar pressurizado e é utilizado em várias funções dos caminhões, como frenagem e troca de marchas. Os atributos não foram nomeados por conta da privacidade da empresa. Os códigos foram desenvolvidos em linguagem de programação Python na plataforma Google Colab. Vamos para a implementação:

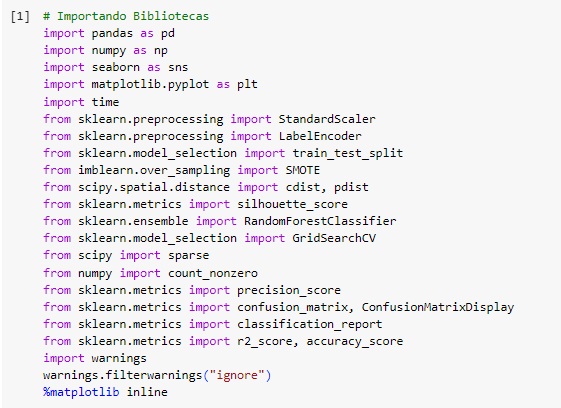
Vamos começar importando as bibliotecas.

Warnings – para avisos de alertas;

Pandas – para análise e manipulação de dados;

Numpy – para realizar operações em arrays multidimensionais;

Seaborn – para visualizar gráficos;

Matplotlib – para visualizações mais interativas;

Scikit-learn – para aplicar modelos de machine learning;

Time – para funcionalidades referente ao tempo;

Smote – para o balanceamento dos dados.

Em seguida vamos carregar os dados e observá-los.

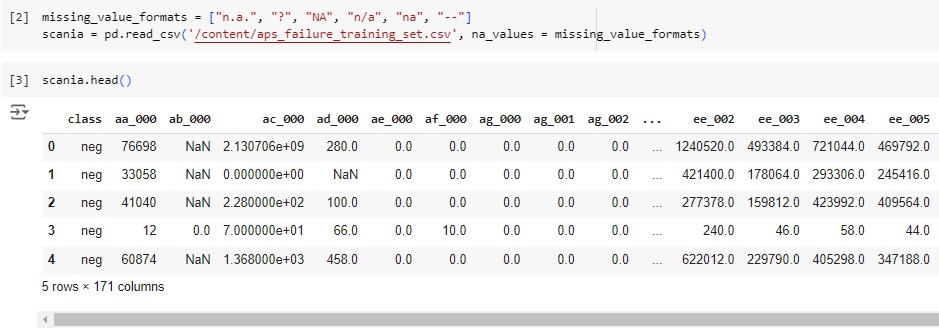
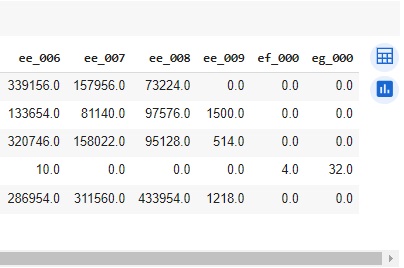
Observando o shape notamos que a base de dados possui 60000 linhas e 171 colunas.

Com a ajuda do comando info(), obtemos algumas informações informações e percebemos que existem variáveis do tipo object, que mais adiante serão tratadas.

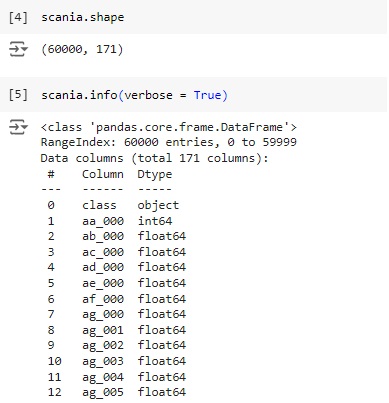
Vamos observar a nossa variável target ‘class’. Percebemos através do gráfico que ela esta bem desbalanceada, logo mais iremos cuidar disso.

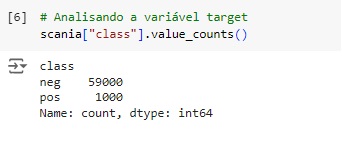
Com a ajuda do comando duplicated() percebemos que não existe valores duplicados. Verificando o total de valores nulos o comando isnull().sum().sum(). Podemos observar que existem muitos valores nulos no banco de dados para serem tratados. Já na variável alvo não existem valores faltantes.

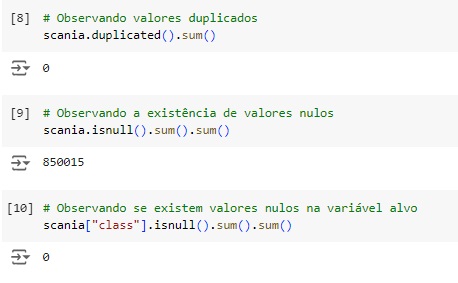
Agora, com a ajuda do describe(), vamos observar informações estatísticas, como média, mediana e desvio padrão. Também podemos notar que os dados estão em diversas escalas, logo mais iremos normalizar estes dados.

Vamos observar graficamente os valores nulos.

Agora vamos calcular os valores ausente em cada variável, se existir variável com 70% dos valores ausentes iremos dropar(apagar) a coluna, caso contrário faremos o tratamento dos dados. Percebemos que existem colunas com valor igual ou maior que 70%.

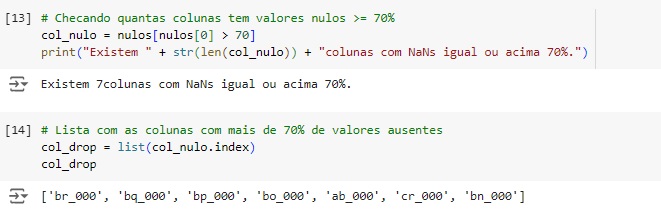
Apagando as 7 colunas com valor ausente igual ou maior do que 70% utilizando o comando drop().

Vamos substituir os valores nulos nas outras variáveis pela mediana e conferir as mudanças. Percebemos que os valores foram tratados com sucesso.

Agora vamos analisar a dispersão do dataset. Para que um dataset seja esparso aproximadamente metade das observações ou mais da metade delas deve ser zero. Percebemos que temos 30% que é um valor elevado, mas ainda longe dos 50%. Através da função do scipy issparse() temos como resposta que o conjunto de dados não é esparso, consta como False. Vamos substituir os valores nulos nas outras variáveis pela mediana e conferir as mudanças. Percebemos que os valores foram tratados com sucesso.

Carregando as variáveis categóricas, percebemos que existe apenas uma, que é a nossa variável target.

Vamos carregas as variáveis numéricas para o boxplot e analisarmos se existem outliers. Através dos gráfico notamos que existem muitos.

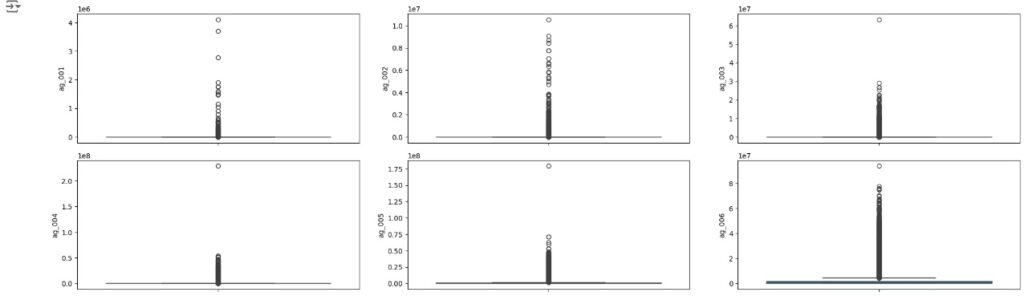
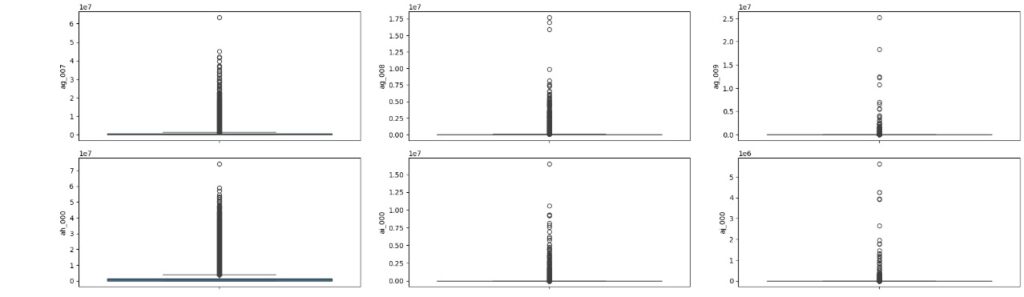
Vamos resolver o problema dos outliers utilizando o método Tukey ou Boxplot onde iremos definir os limites inferior e superior a partir do interquartil (IQR) e dos primeiros (Q1) e terceiros (Q3) quartis.

Quartis são separatrizes que dividem um conjunto de dados em 4 partes iguais. O objetivo das separatrizes é proporcionar uma melhor ideia da dispersão do dataset, principalmente da simetria ou assimetria da distribuição.

O limite inferior é definido pelo primeiro quartil menos o produto entre o valor 1.5 e o interquartil.

Linf = Q1 – (1.5 * IQR)

O limite superior é definido pelo terceiro quartil mais o produto entre o valor 1.5 e o interquartil.

Lsup = Q3 + (1.5 * IQR)

Em seguida vamos observar se os outliers foram removidos através do boxplot.

Esta função serve para substituir os outliers, onde valores acima do limite superior são substituídos pelo próprio limite superior e valores abaixo do limite inferior são substituídos pelo próprio limite inferior.

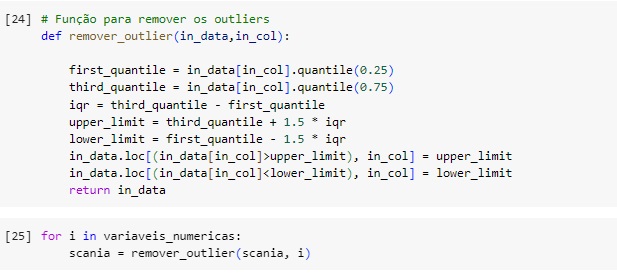
No gráfico abaixo podemos perceber que os outliers foram tratados com sucesso.

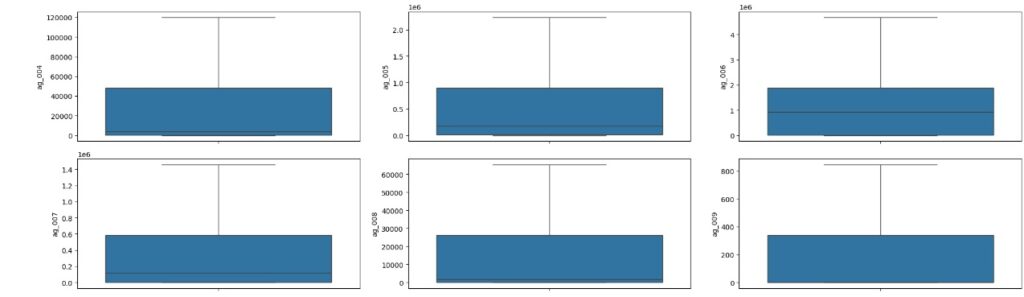
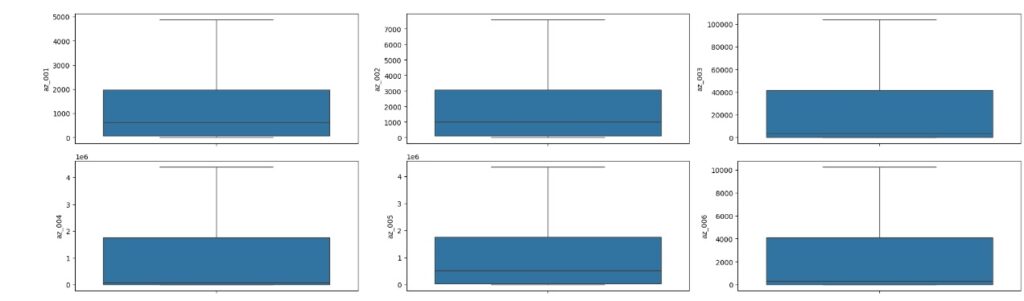
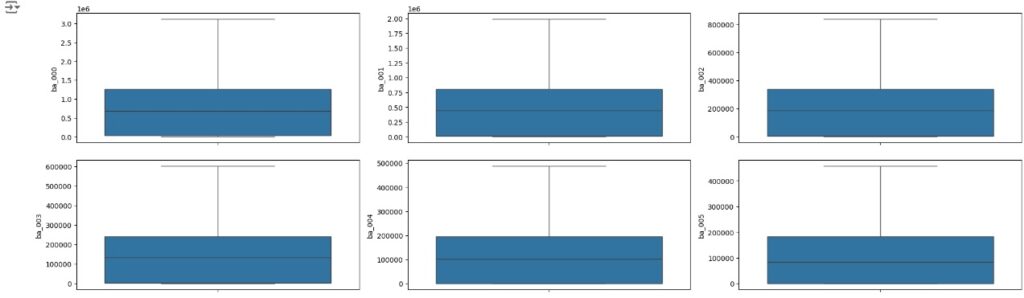
Podemos notar que a maioria das variáveis possuem apenas um valor dominante, devido a isso não oferecem variabilidade e informações ao modelo podendo causar o overfitting que é o ajuste excessivo dos dados. Portanto estas variáveis serão removidas.

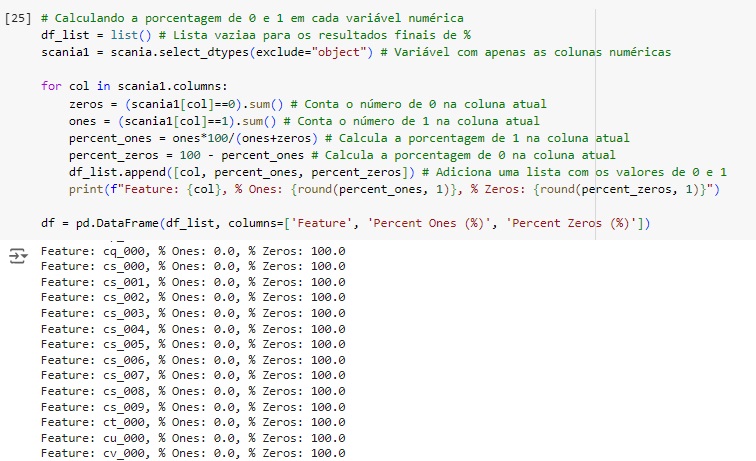
Vamos encontrar as colunas que possuem 99% valores 0 e 1. Percebemos que são 155 variáveis. Vamos excluir estas variáveis com o comando drop().

Observando o shape e o dataframe atualizado.

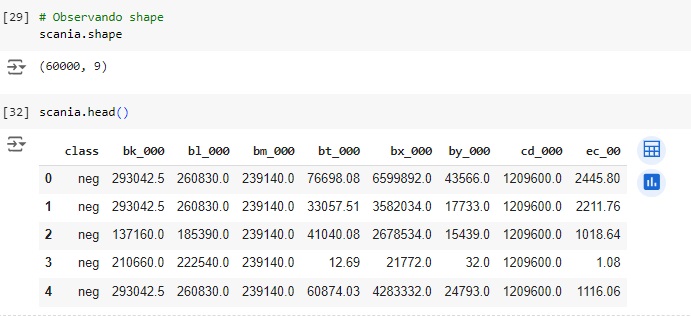
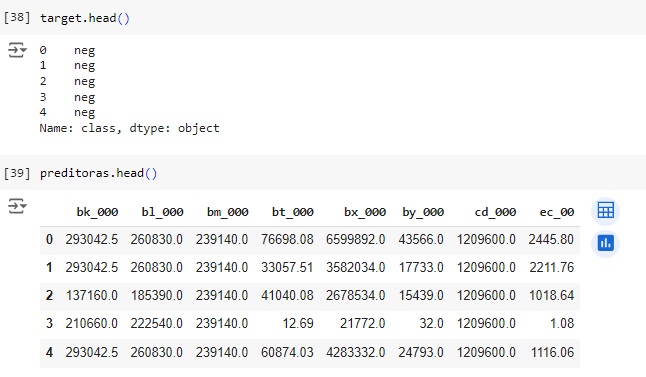
Observando o shape da variáveis target e preditoras.

Agora vamos balancear os dados com o SMOTE(), o comando vai avaliar o banco de dados e vai criar novos dados para igualar as variáveis target. Em seguida vamos aplicar o balanceador, vamos criar duas novas variáveis preditoras_res e target_res que serão os resultados do balanceamento, em seguida usaremos o fit_resmple() que é o método balanceador do SMOTE(), e passamos os parâmetros que queremos balancear, no caso preditoras e target.

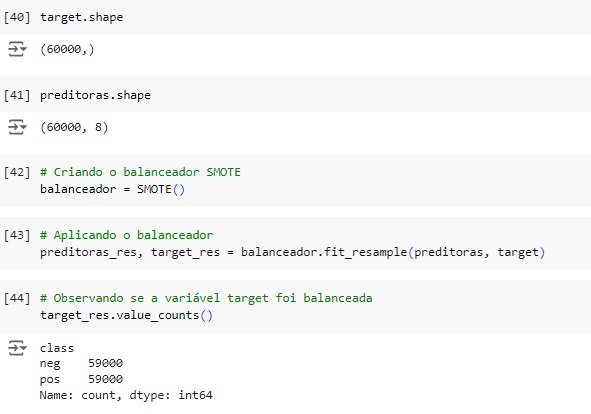
Visualizando através do gráfico, percebemos que a variável target foi balanceada corretamente.

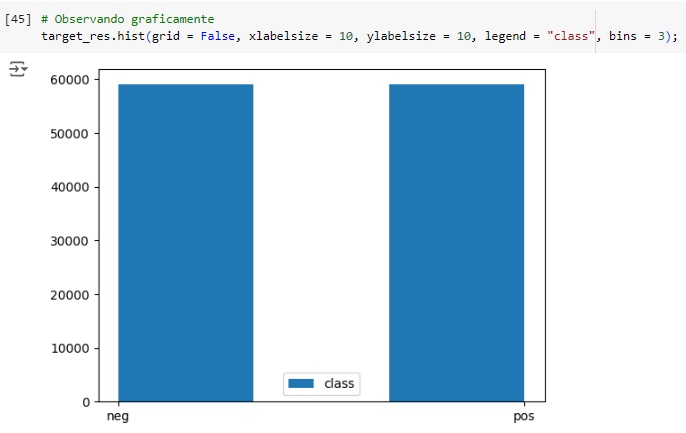
Vamos observar a quantidade de dados após o balanceamento, percebemos que foi para 118000.

Usando o train_test_split() vamos dividir a base de dados em treino e teste, sendo 70% dos dados para treinamento e 30% para teste.

Em seguida vamos padronizar os dados das variáveis preditoras para colocá-los na mesma escala, vamos utilizar o StandardScaler() e o fit_transform() para isso.

Observando os dados padronizados.

Criando o classificador com o algoritmo de machine learning RandomForestClassifier() com alguns hiperparâmetros para melhorar a acurácia do modelo, n_estimators = 100 é o número de árvores de decisão que terá o modelo. Em seguida criamos o modelo, passamos o classificador com o comando fit() e passamos como parâmetro as variáveis de treino padronizadas.

Olhando a acurácia do modelo, percebemos que tivemos 97,74% de acurácia.

Comparando as previsões com os dados reais percebemos que o algoritmo acertou as 3 primeiras…

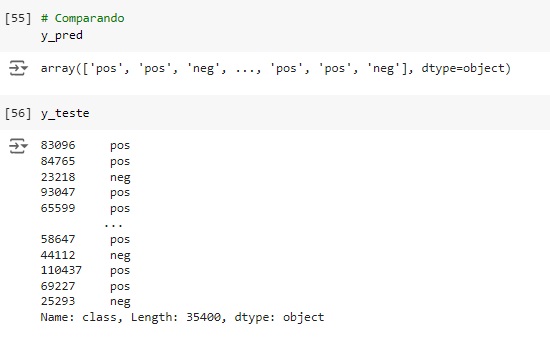
Através do classification report percebemos que o algoritmo consegue identificar corretamente 96% onde não existe falha (recall 0.96) e quando identifica a precisão é de 0.99% (precision 0.99). Para as falhas o resultado do algoritmo foi de 0.99% das identificações corretas (recall 0.99) com 99% de certeza (precision 0.96).

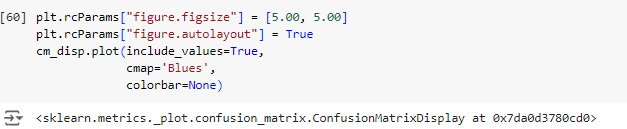
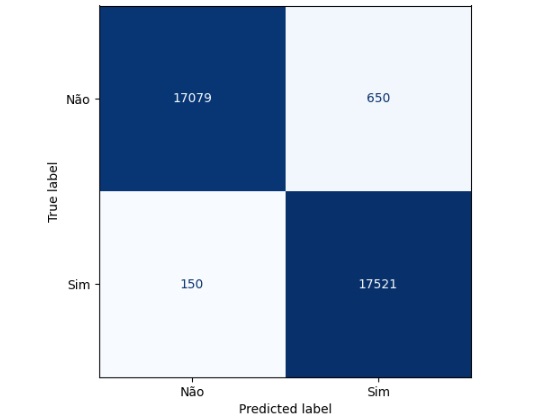
Plotando a matriz de confusão podemos perceber que 17079 itens não possuem falhas no banco de dados real e foi também o valor que o modelo previu, ou seja, é um verdadeiro positivo. No outro lado da matriz percebemos que segundo os dados reais existem 17521 falhas, o mesmo valor que o modelo previu. Com isso conseguimos perceber que a diagonal que está azul mais escuro são os acertos do modelo.

Passando para a diagonal azul claro, percebemos que o banco de dados real tem 650 sem falhas, mas o modelo previu que tem, ou seja, é um falso positivo, no caso o modelo errou a previsão. Na outra diagonal percebemos que tem 150 falhas no banco de dados real, mas o modelo previu que não havia falha.