Modelo Preditivo Para o Não Cancelamento de Assinatura – KNN

Como de costume, vamos mostrar mais um projeto preditivo de machine learning, neste projeto vamos prever o cancelamento da assinatura de uma operadora de TV a cabo. Para tal vamos usar o algoritmo KNN. Primeiro vamos ter uma pequena noção do funcionamento do KNN e em seguida iremos para a implementação.

O Algoritmo KNN

O algoritmo K-Nearest Neighbors (KNN) é uma técnica amplamente utilizada no campo do machine learning. Ele pertence à categoria de algoritmos de aprendizado supervisionado e é usado para classificação e regressão. É um método não paramétrico que se baseia na proximidade dos exemplos de treinamento para tomar decisões de classificação ou regressão. Ele assume que instâncias similares estão próximas umas das outras no espaço de características. Em outras palavras, se um ponto está perto de outros pontos de uma determinada classe, é mais provável que ele também pertença a essa classe

O termo “K” em KNN se refere ao número de vizinhos mais próximos considerados para tomar uma decisão. Por exemplo, se K é igual a 3, o algoritmo irá verificar os três vizinhos mais próximos e atribuir ao novo exemplo a classe mais frequente entre esses vizinhos. Isso significa que a escolha do valor de K é um fator crucial no desempenho do algoritmo.

Uma das principais vantagens do KNN é que ele não requer uma fase de treinamento complexa, pois utiliza diretamente os exemplos de treinamento para tomar decisões. Além disso, é um algoritmo relativamente simples de entender e implementar. No entanto, ele pode ser computacionalmente caro quando o conjunto de dados é grande, pois ele precisa calcular a distância entre cada exemplo e todos os outros exemplos do conjunto de treinamento.

Para implementar o algoritmo KNN em um projeto de machine learning, é necessário definir a métrica de distância utilizada para calcular a proximidade entre os exemplos. A métrica mais comumente utilizada é a distância euclidiana, mas outras métricas também podem ser utilizadas dependendo do domínio do problema. Além disso, é importante normalizar os dados antes de aplicar o KNN, para evitar que características com escalas diferentes dominem o cálculo da distância.

Então, depois de uma breve teoria, vamos para a implementação. Os código foram desenvolvidos em linguagem Python utilizando a plataforma Google Colab.

Vamos começar importando as bibliotecas:

Pandas – para análise e manipulação de dados;

Numpy – para realizar operações em arrays multidimensionais;

Seaborn – para visualizar gráficos;

Matplotlib – para visualizações mais interativas;

Scikit-learn – para aplicar modelos de machine learning;

Time – para funcionalidades referente ao tempo.

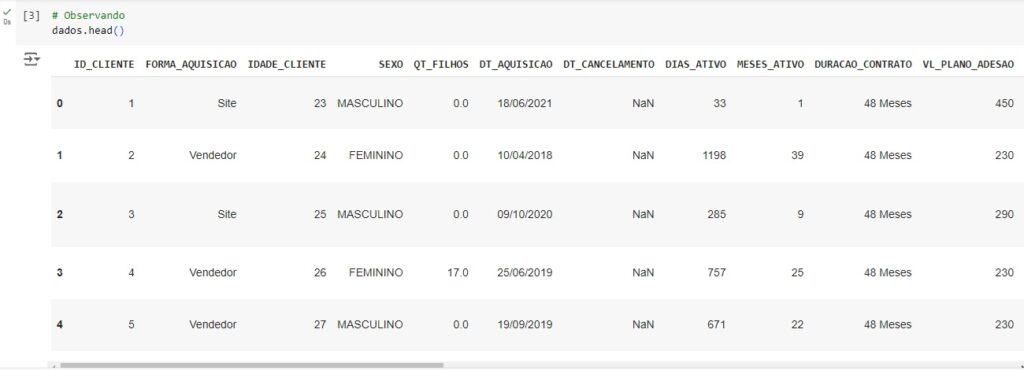
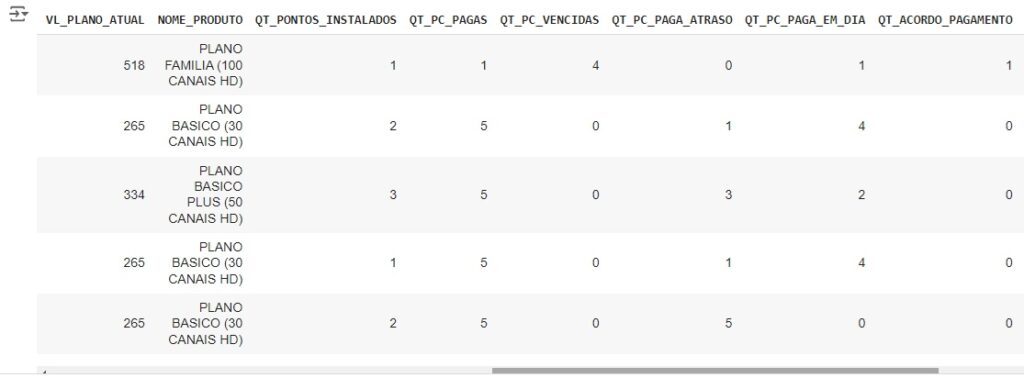
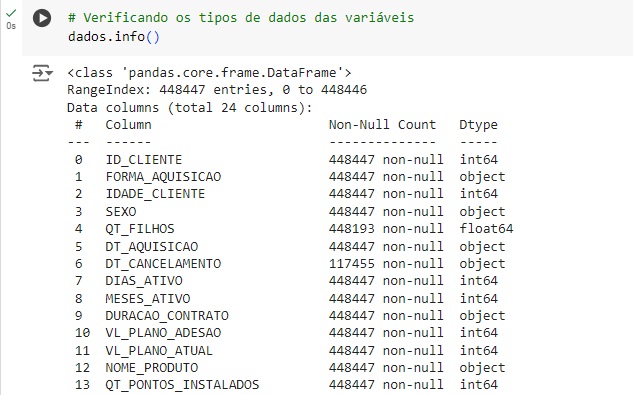
Através do comando shape percebemos que o banco de dados possui 448447 linhas e 24 colunas. Percebemos também com ajuda do comando info() que temos algumas variáveis categóricas, que mais para frente serão tratadas para o melhor funcionamento do algoritmo de machine learning.

Aqui podemos observar o período de tempo no qual os dados foram coletados, de 01/01/2001 até 29/06/2021. Para isso, usamos o pacote date() para encontrar a data mínima e máxima.

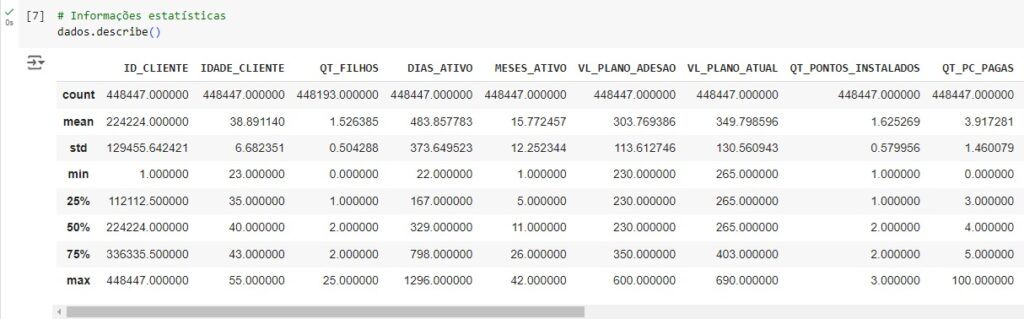
Agora, com a ajuda do describe(), vamos observar informações estatísticas, como média, mediana e desvio padrão. Também podemos notar que os dados estão em diversas escalas, logo mais iremos padronizar estes dados.

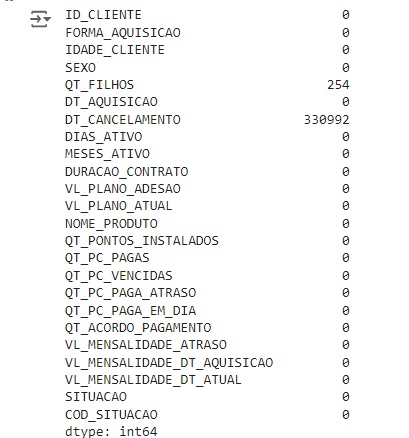
Vamos verificar quantos valores estão faltando em cada coluna com o comando isna().sum(). Percebemos que a variável DT_CANCELAMENTO tem uma grande quantidade de valores nulos, mas isso não é importante, pois iremos deletar esta coluna, pois ela não é necessária. Já na variável QT_FILHOS consta 254 valores em branco e deverá ser tratada, por ser uma variável importante.

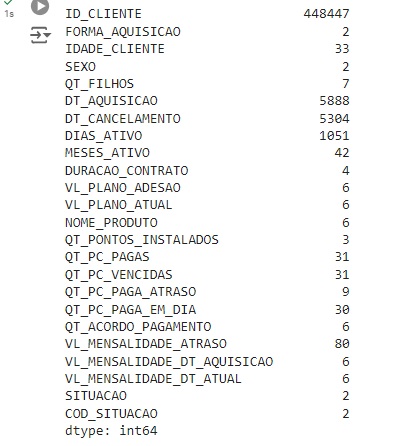
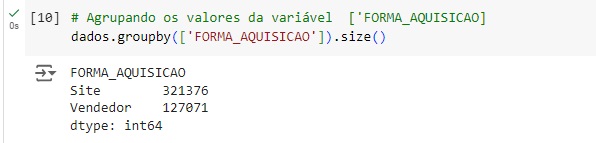
Com o comando groupby(), faremos um agrupamento de uma variável e com o comando size() vamos contar os valores. Na variável FORMA_AQUISIÇÃO temos 321376 registros de observações via site e 127071 forma de aquisição via vendedor.

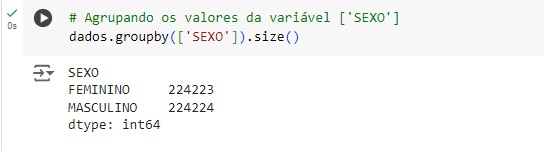
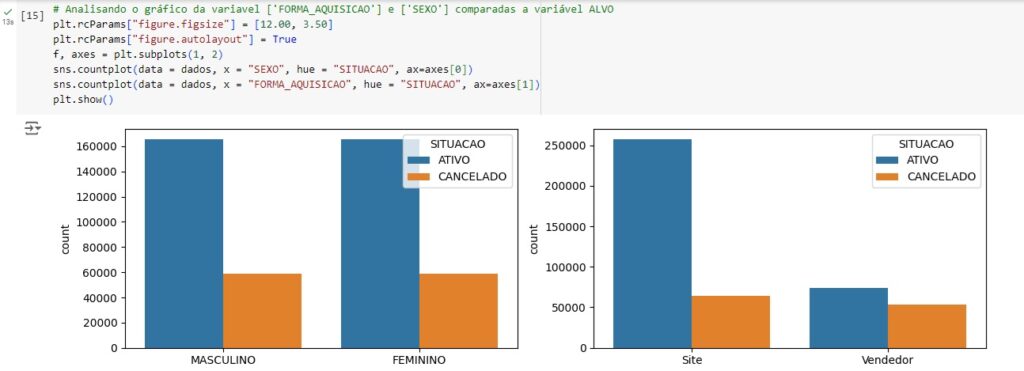
Fazemos o mesmo para a variável SEXO.

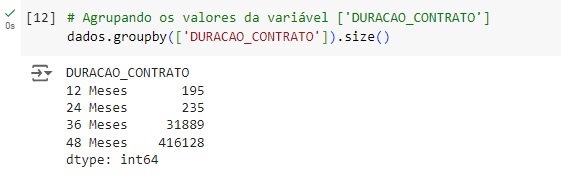
E também para a variável DURACAO_CONTRATO, onde se percebe que temos apenas 4 tipos de contrato.

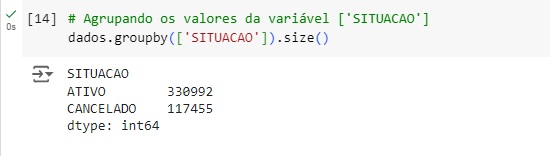
Observando graficamente as variáveis agrupadas acima.

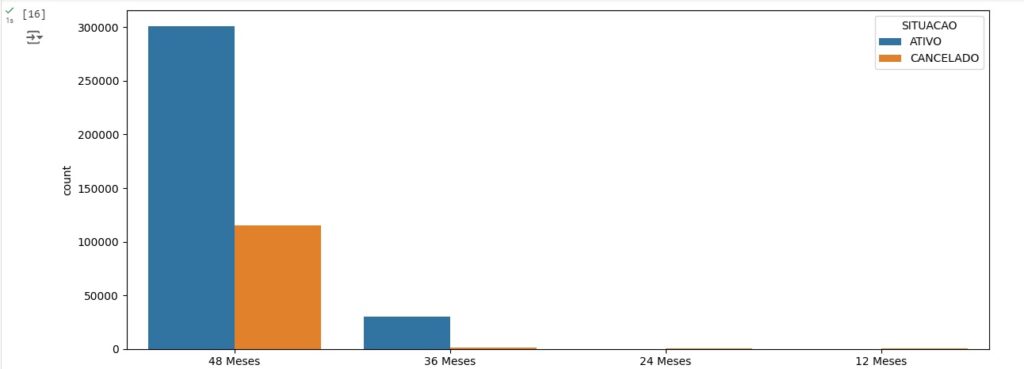
Aqui notamos que o maior tempo de duração são nos planos de 48 meses.

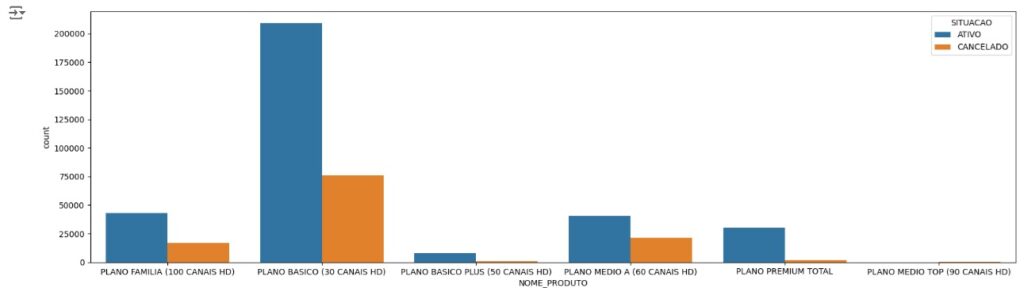
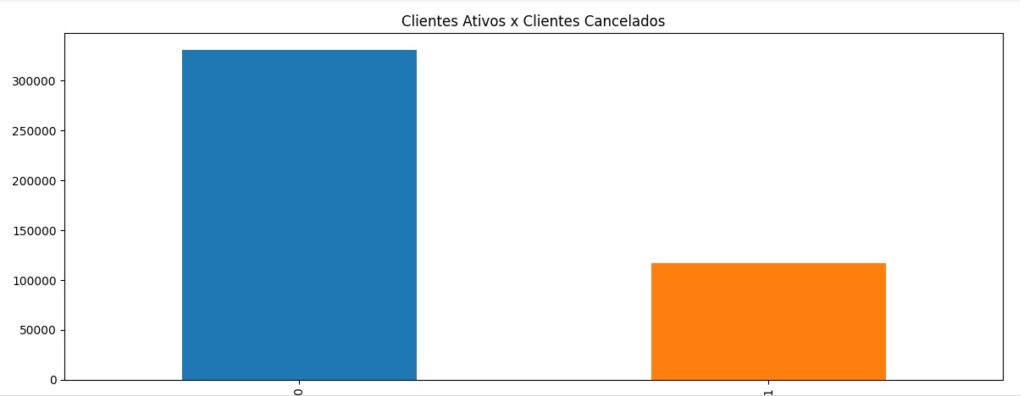
Aqui observamos os clientes ativos e os cancelados, notamos o desbalanceamento da variável, pois temos um número muito maior de clientes ativos do que cancelados.

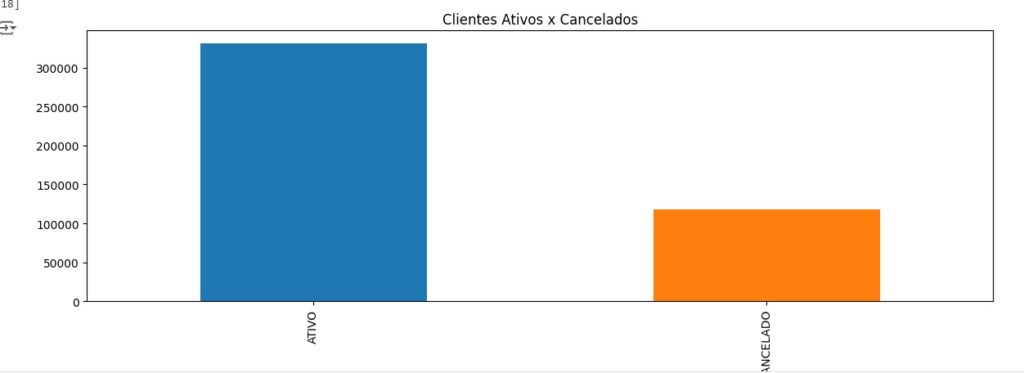
Analisando as variáveis numéricas.

Vamos criar um boxplot para observar outliers que são os valores discrepantes. Os outliers são os pontos escuros que aparecem em cada gráfico. Percebemos que no gráfica da variável QT_FILHOS, através dos pontos escuros identificamos pessoas com mais de 15 e 20 filhos, algo que não é normal, portanto, podemos considerar um outlier.

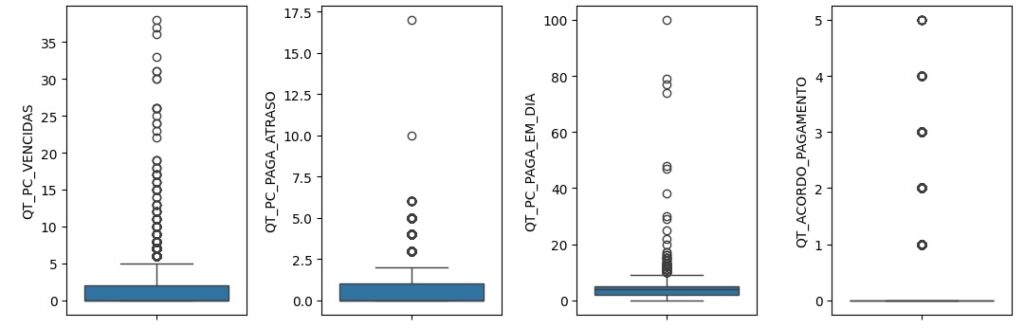
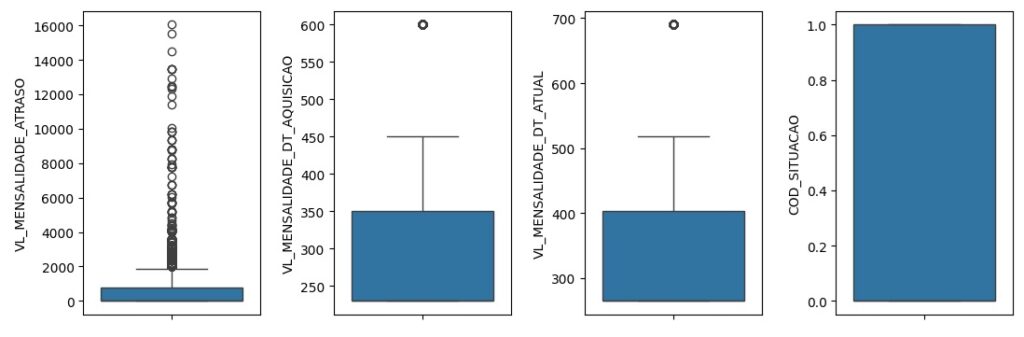
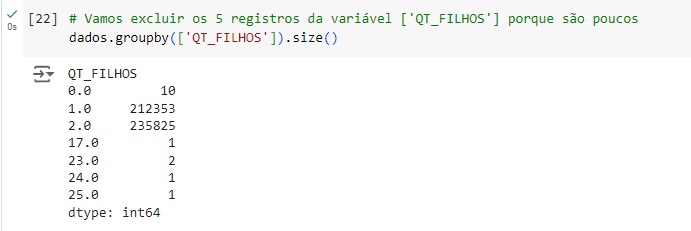
Notamos que temos apenas 5 registros dentro de um volume de mais de 440 mil registros, dessa forma iremos exclui-los mais adiante pois não irá causar impacto de perda de dados, pois a quantidade é muito pequena comparada ao total de registros. Temos 1 pessoa com 17 filhos, 2 pessoas com 23, 1 com 24 e 1 com 25.

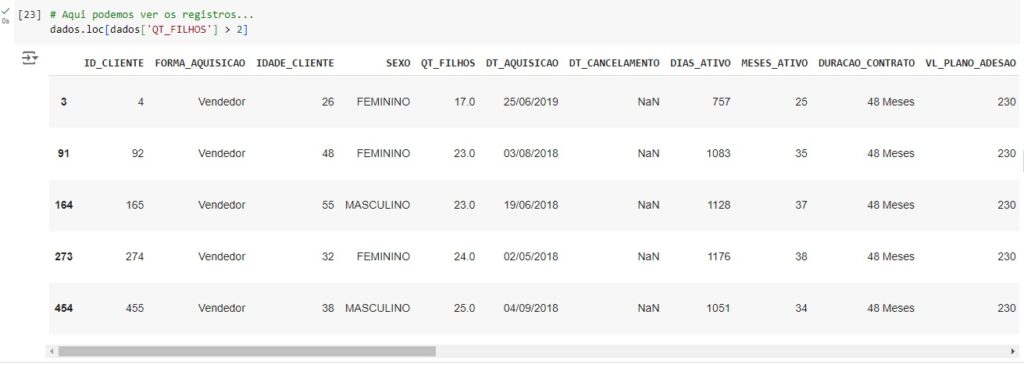
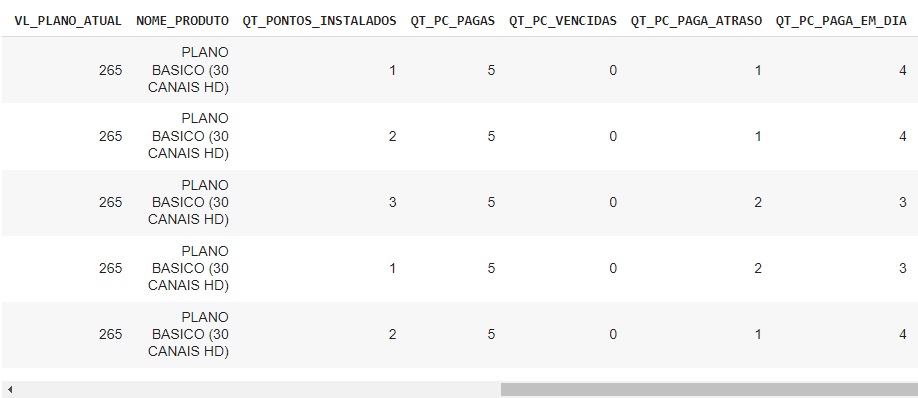
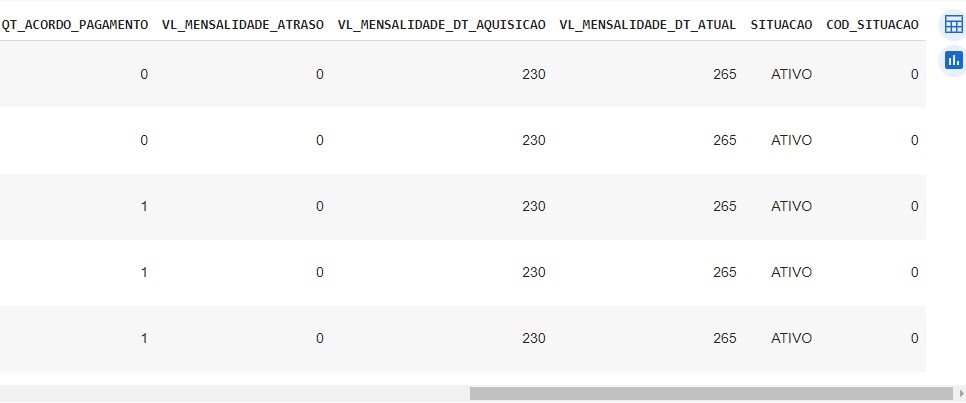
Aqui podemos observar os 5 registros com outliers.

Com o novo banco de dados df_dados vamos filtrar na variável QT_FILHOS todos os valores que forem <= 2, desta forma os outliers já serão excluídos.

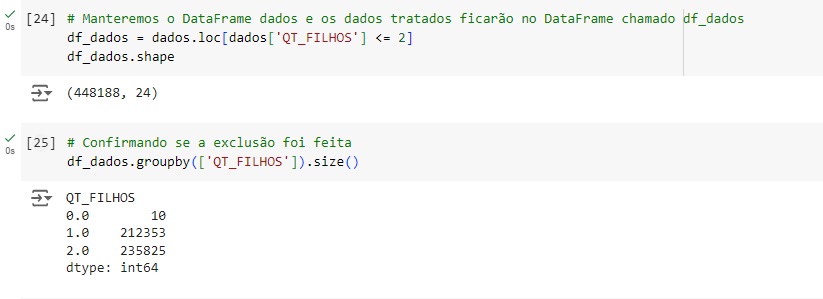
Na variável QT_FILHOS também existem 257 valores em branco que precisam ser tratados. Para isto vamos observar a média, mediana e moda.

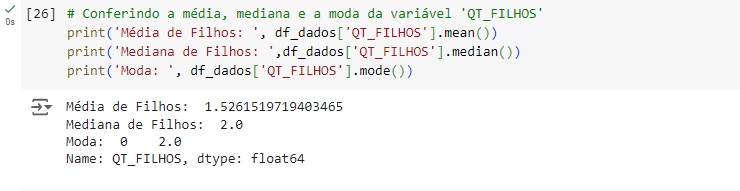
Vamos inserir a mediana no lugar dos valores nulos da variável QT_FILHOS. Em seguida podemos perceber que não existem mais valores nulos na variável.

Vamos tratar a variável DURACAO_CONTRATO para que ela tenha apenas o valor dos meses, para isso vamos usar o comando replace() que vai substituir onde estiver ’12 Meses’ apenas por ’12’, e assim por diante.

Vamos observar se a modificação foi feita.

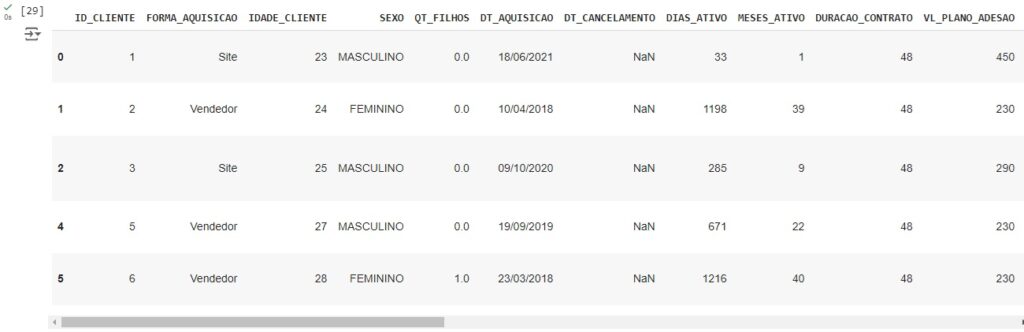
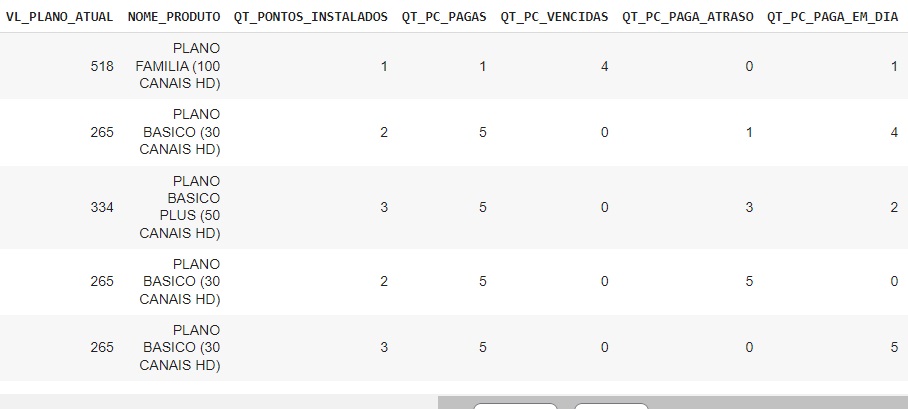
Percebemos que na variável DURACAO_CONTRATO o valor já consta como int64.

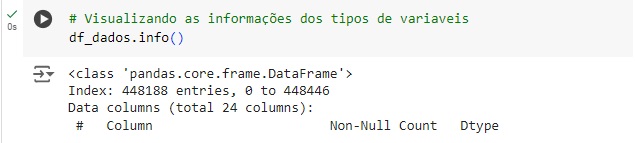
Nesta etapa vamos substituir os valores que ultrapassam o tempo máximo de contrato que é 48 meses. Logo abaixo podemos perceber que as variáveis foram ajustadas, o valor maior está como 48.

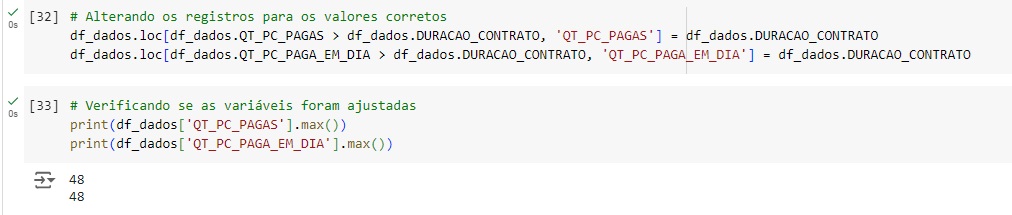
Agora vamos fazer uma engenharia de atributos. Então vamos começar criando uma variável chamada NIVEL_PAGAMENTO que será de acordo com as parcelas pagas. Vamos categorizá-la criando uma lista com bins (que são as quantidades de valores nas quais estamos interessados, no caso 4), no bins temos que deixar um valor menor a mais no caso -100. Aqui teremos também uma lista com labels onde será representado 3 – ‘RUIM’, 6 – ‘MEDIO’, 12 – ‘BOM’ e 48 – ‘OTIMO’. Estes valore são baseados na variável QT_PC_PAGAS, ou seja, se um cliente pagou até 3 parcelas, ele tem um nível de pagamento ruim, se ele pagou 6 parcelas, tem um nível de pagamento médio e assim por diante. Estamos criando faixas de valores e para isso usamos a função cut(). Em seguida com o value.counts(), vamos contar quantas clientes temos em cada nível de pagamento, e percebemos que o nível ‘MEDIO’ é o que mais tem pessoas totalizando 297750, e o nível ‘OTIMO’ é o que tem menos com apenas 38 pessoas.

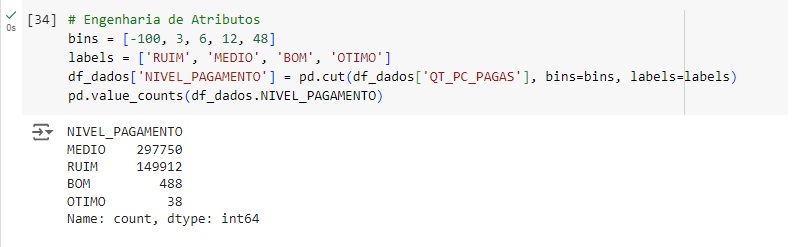
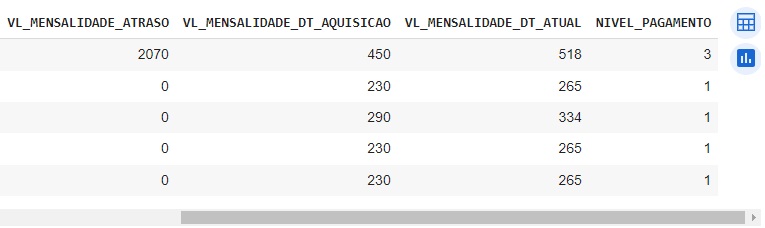
Observando o banco de dados, notamos que no final a nova variável NIVEL_PAGAMENTO foi adicionada com cada nível que definimos acima.

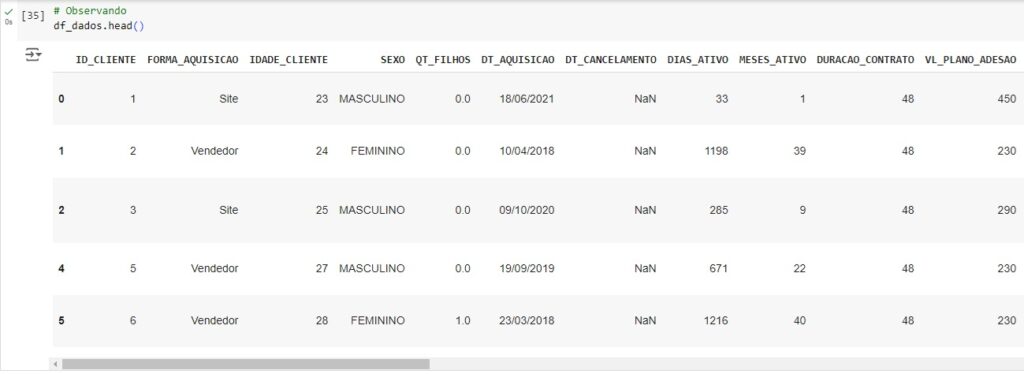
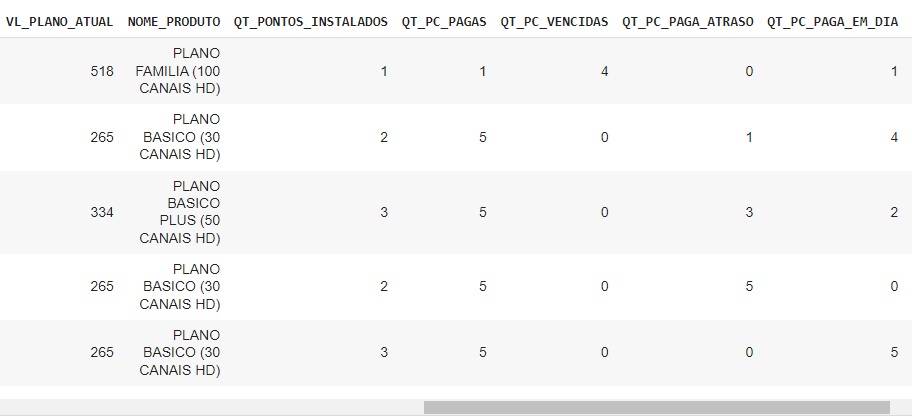
Por uma questão de segurança, vamos fazer uma cópia do nosso banco de dados com os tratamentos já feitos.

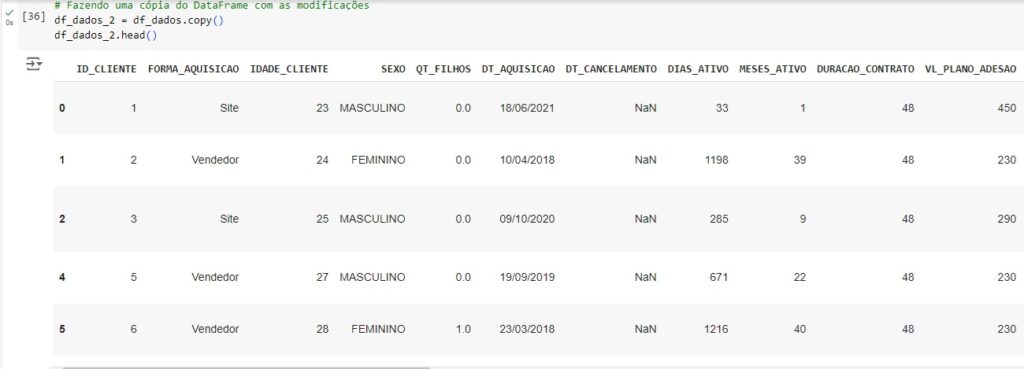
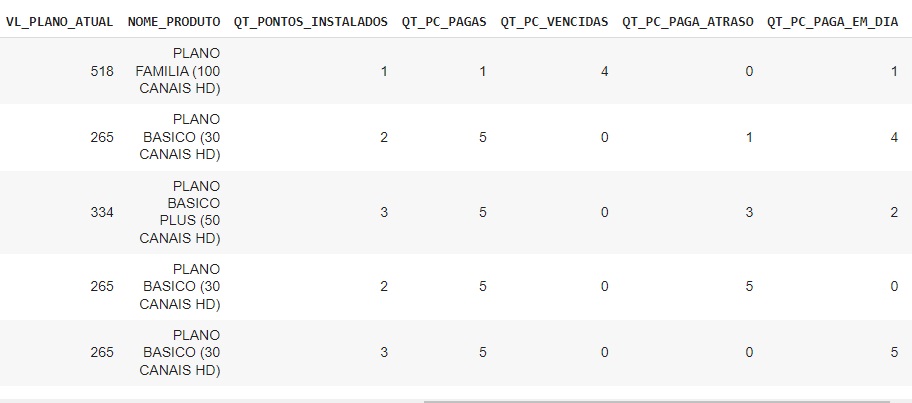
Agora vamos transformar as variáveis categóricas em numéricas utilizando o OneHotEncoder através da biblioteca do scikit-learn LabelEncoder(). Vamos passar o comando lb.fit_transform() nas variáveis que queremos converter.

Observando as transformações.

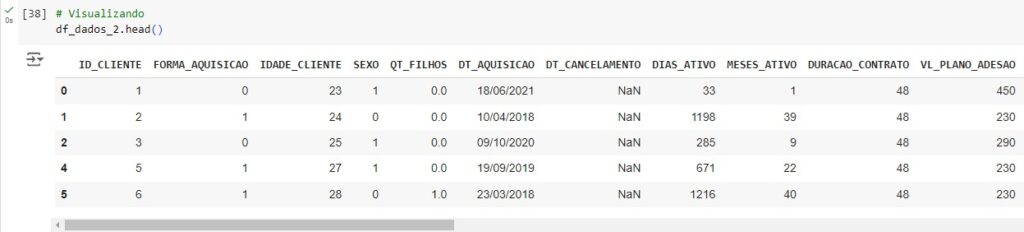
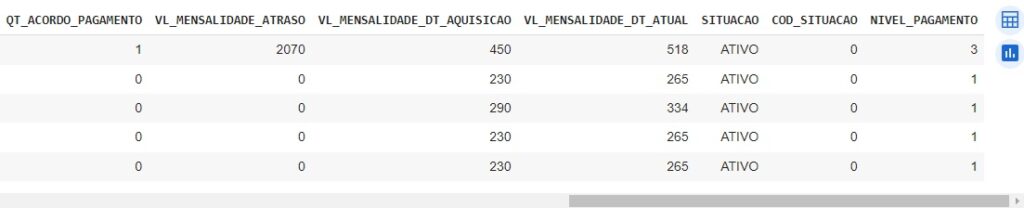
Vamos filtrar as colunas e criar um novo banco de dados chamado df_dados_2 com as colunas necessárias para aplicar o modelo de machine learning.

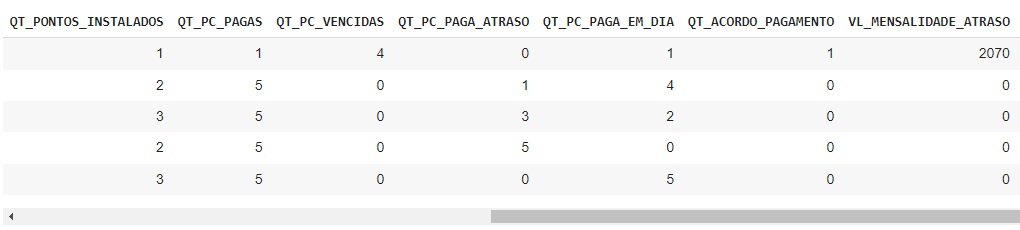
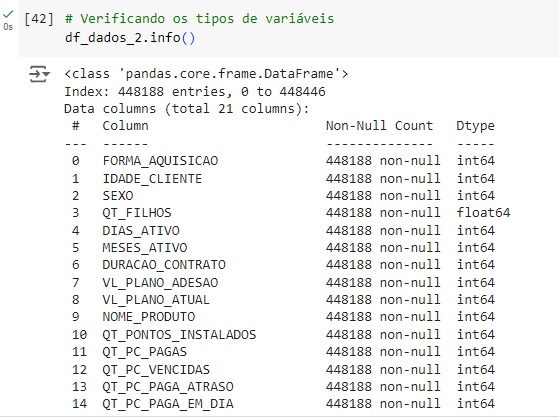
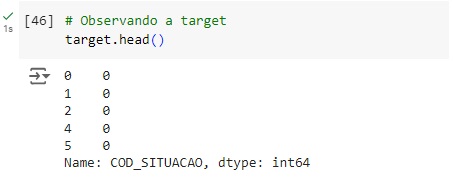
Vamos separar as variáveis preditoras da variável target COD_SITUACAO. Vamos criar um novo banco de dados chamado preditoras e outro chamado target.

Vamos usar o SMOTE() para criar o balanceador e equilibrar os dados. Depois vamos aplicar o balanceador com o comando fit_resample() que vai reamostrar os dados de acordo com as variáveis e vai montar um novo conjunto de dados maior.

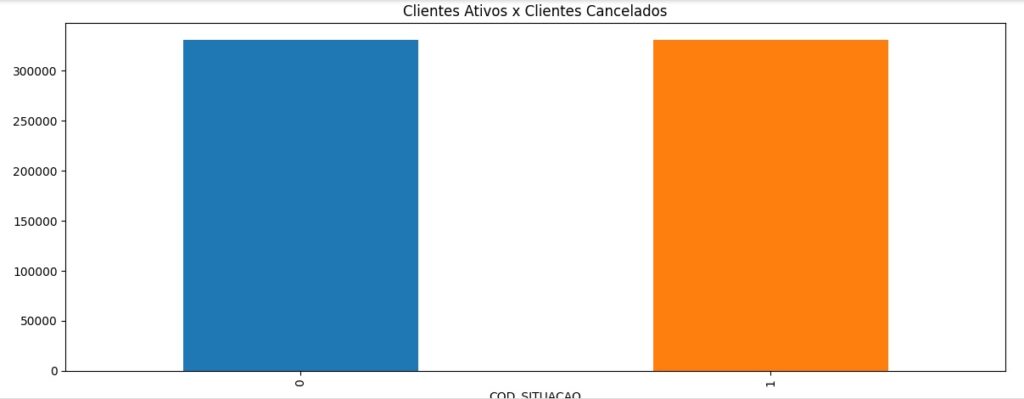
Observando se o balanceamento ocorreu. Notamos que os dados estão balanceados.

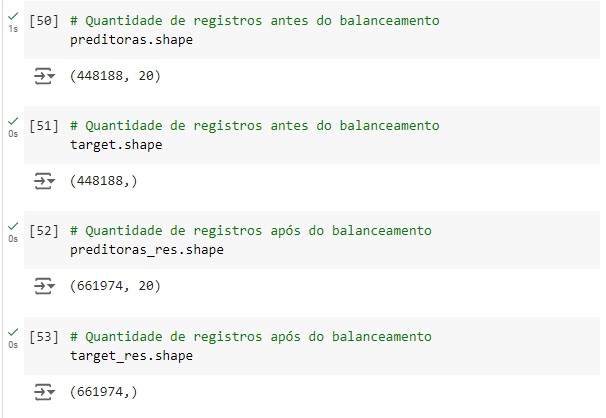
Usando o train_test_split() vamos dividir a base de dados em treino e teste, sendo 70% dos dados para treinamento e 30% para teste.

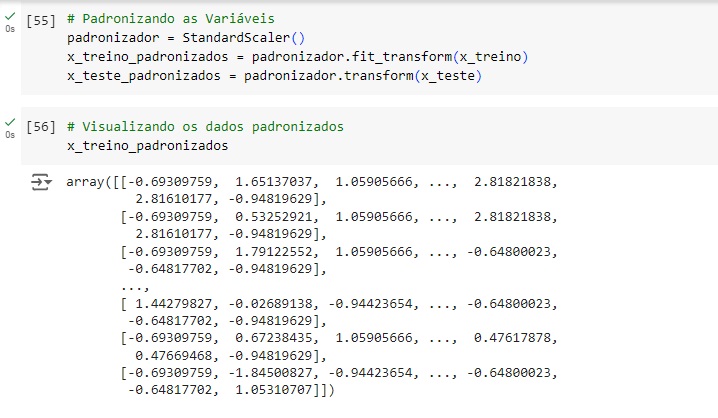
Agora vamos padronizar os dados das variáveis preditoras para colocá-los na mesma escala, vamos utilizar o StandardScaler() para isso. Com isso, os dados deixam de ser dataframe para se tornarem arrays.

Agora vamos criar uma variável chamada kVals, que significa valor de k que significa número de vizinhos. Vamos criar um range de 3 até 10 indo de 2 em 2. Então o range terá os valores 3, 5, 7 e 9. teremos estes 4 modelos rodando simultaneamente para avaliar qual o melhor parâmetro. Em seguida criamos uma lista vazia com as acurácias.

Agora colocamos uma variável start = time.time() para medir o tempo que inicia. dentro do loop for temos a criação e o teste do modelo preditivo para analisar qual o melhor hiperparâmetro. Quando no nosso loop o valor de k for 3 ele vai testar no algoritmo KNeighborsClassifier(n_neighbors = k), vai passar o número de vizinhos k, vai treinar o modelo e em seguida vai avaliar e mostrar o resultado com cada valor de k.

Nos resultados finais percebemos que o melhor parâmetro foi com o valor de k = 3 que teve 97.68% de acurácia.

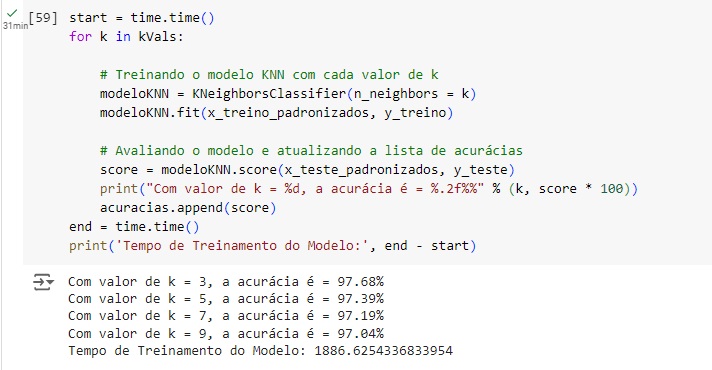
Somente confirmando a melhor acurácia. Percebemos que o k = 3 é o melhor parâmetro para o modelo final.

Agora finalmente vamos testar o modelo e ver a acurácia, vamos usar o accuracy_score() passando a variável target y_teste que são os valores originais e as previsoes que são os valores previstos pelo modelo KNN.

Podemos observar que a acurácia foi de 97%, ou seja a cada 100 previsões realizadas, o modelo acerta 97.