Prevendo Falhas de Máquinas

As máquinas são muito importantes para o bom funcionamento operacional das fábricas, então vamos criar um modelo preditivo para prever as falhas de algumas máquinas de uma indústria, para isto vamos utilizar dados coletados de sensores de várias máquinas. Os códigos foram desenvolvidos em linguagem Python na plataforma Google Colab. Antes de começar vamos analisar algumas informações sobre o dataset.

footfall: O número de pessoas ou objetos passando pela máquina.

tempMode:  O modo de temperatura ou configuração da máquina.

AQ: Índice de qualidade do ar perto da máquina.

USS: Dados do sensor ultrassônico, indicando medições de proximidade.

CS: Leituras atuais do sensor, indicando o uso de corrente elétrica da máquina.

VOC: Nível de compostos orgânicos voláteis detectado perto da máquina.

RP: Posição rotacional ou RPM (rotações por minuto) das peças da máquina.

IP: Pressão de entrada na máquina.

Temperature: A temperatura operacional da máquina.

fail: Indicador binário de falha da máquina (1 para falha, 0 para nenhuma falha). Target.

Vamos começar importando as bibliotecas.

Warnings – para avisos de alertas;

Pandas – para análise e manipulação de dados;

Numpy – para realizar operações em arrays multidimensionais;

Seaborn – para visualizar gráficos;

Matplotlib – para visualizações mais interativas;

Scikit-learn – para aplicar modelos de machine learning;

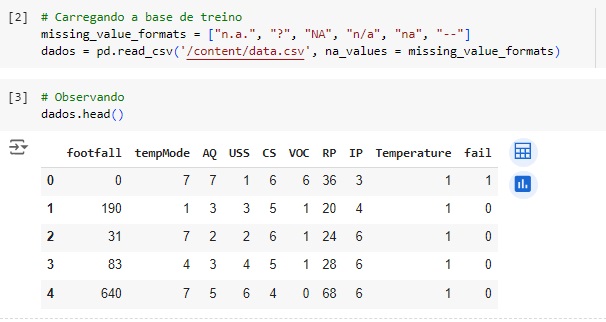
Carregando a base de dados de treino e observando as variáveis. Nossa variável alvo será ‘fail’.

Conferindo o shape, percebemos que o banco de dados possui 944 linhas e 10 colunas.

Com a ajuda do comando info(), obtemos algumas informações e percebemos que existem apenas variáveis do tipo numérico.

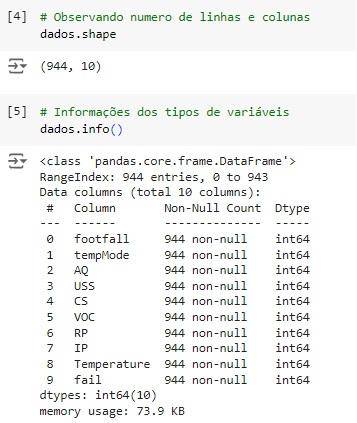
Agora, com a ajuda do describe(), vamos observar informações estatísticas, como média, mediana e desvio padrão.

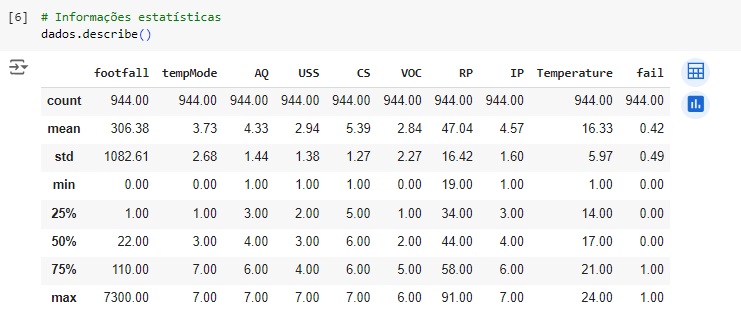
Verificando os valores nulos com o comando isnull().sum(). Podemos observar que não existem valores nulos no dataset. Também vamos usar o comando duplicated().sum() para verificar se existem valores duplicados, podemos perceber que sim, então com o comando drop_duplicates() vamos excluí-lo, e depois conferimos e notamos que já existe mais a duplicidade.

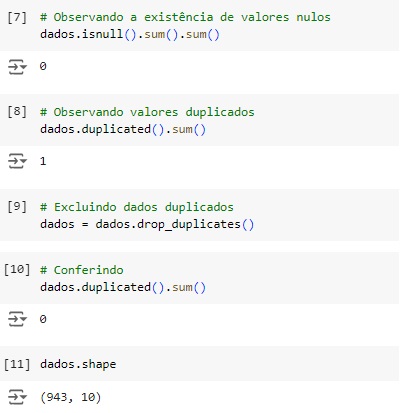
Agora vamos analisar a dispersão do dataset. Para que um dataset seja esparso aproximadamente metade das observações ou mais da metade delas deve ser zero. Percebemos que temos 0.12%. Através da função do scipy issparse() temos como resposta que o conjunto de dados não é esparso, consta como False.

Observando graficamente a variável target percebemos que existe um certo desbalanceamento, mais adiante vamos corrigir este problema.

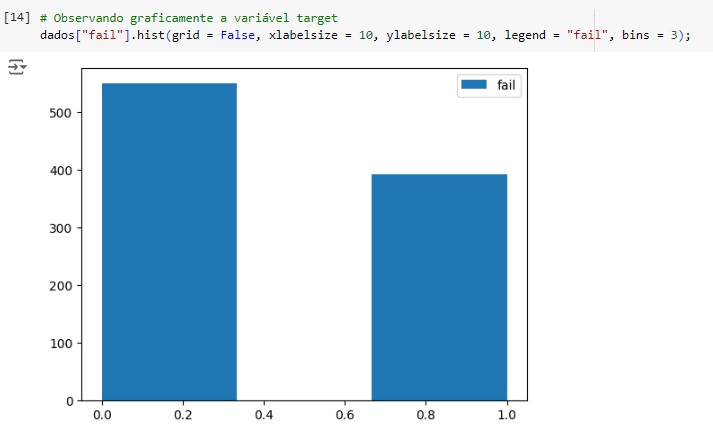
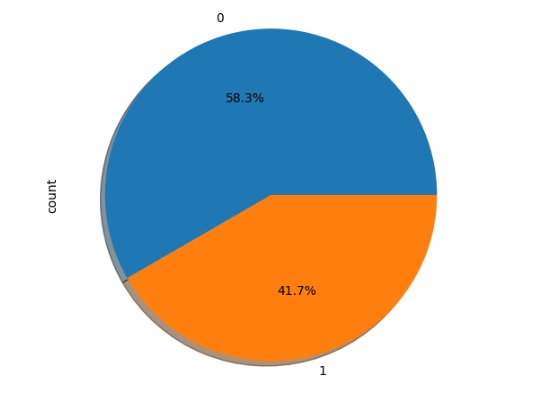
No gráfico abaixo notamos que 58.3% das máquinas não possui falha e 41.7% possui algum tipo de falha.

No gráfico abaixo observamos a distribuição das variáveis.

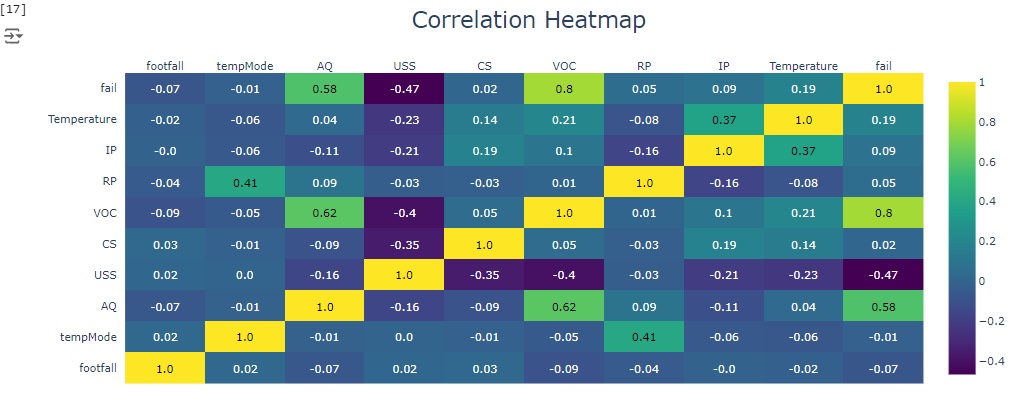
Abaixo temos a matriz de correlação. Através dela podemos notar que existe uma forte correlação positiva entre a variável ‘VOC’ que é o nível de compostos orgânicos voláteis detectado perto da máquina e a variável alvo ‘fail’, assim como a variável ‘AQ’ que é o índice de qualidade do ar perto da máquina também tem uma correlação positiva com a variável target.

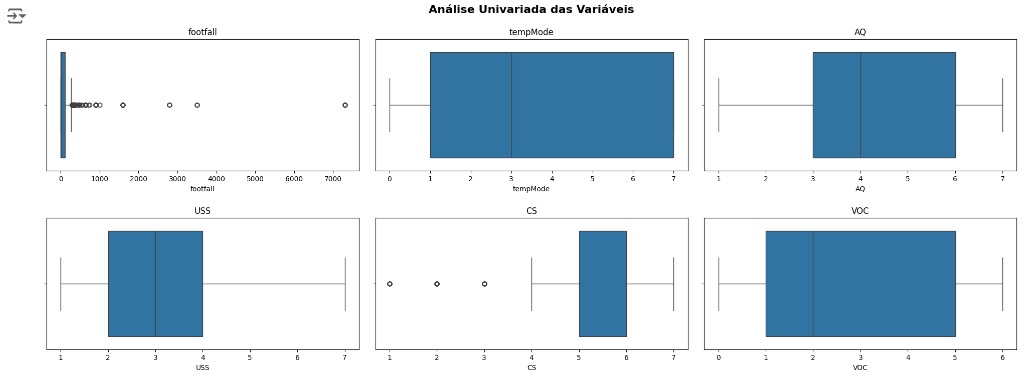
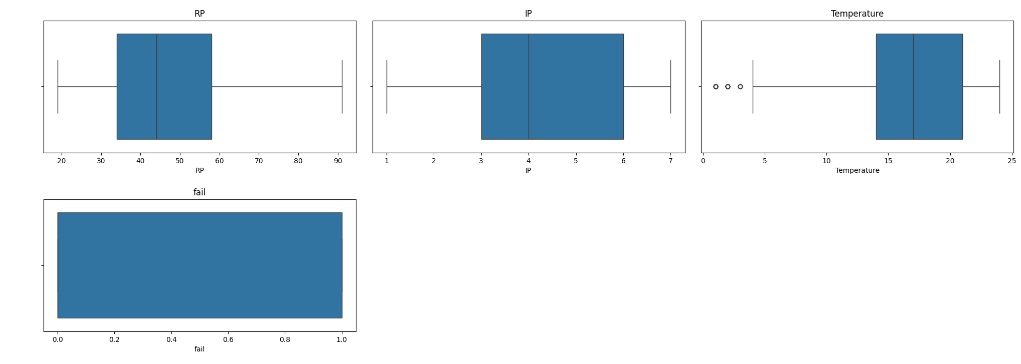
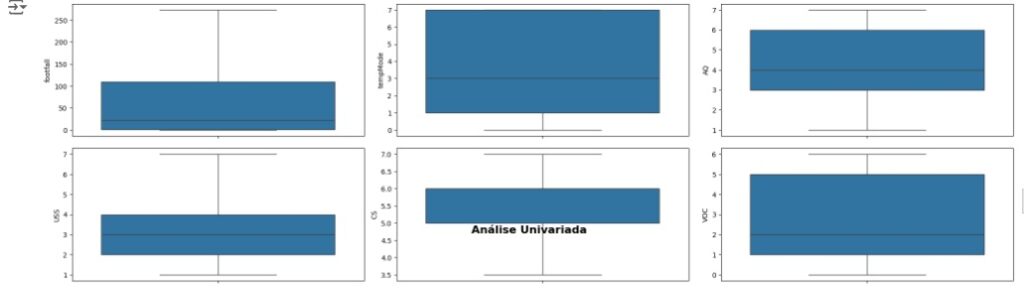
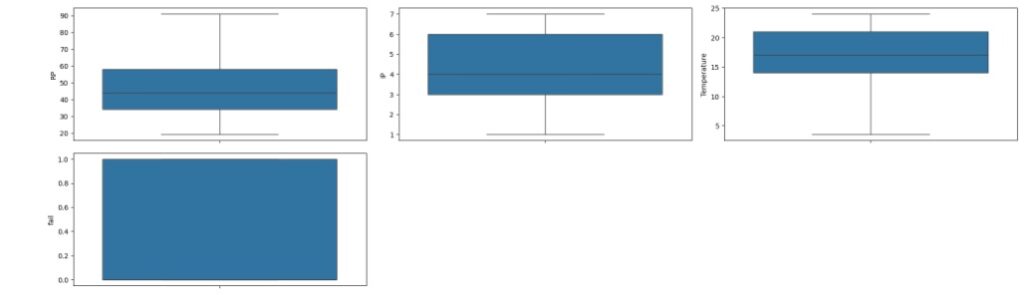
Vamos carregar as variáveis numéricas em um boxplot e observar a existência de outliers. Através dos gráfico percebemos que existem alguns valores discrepantes e em seguida vamos cuidar disto.

Vamos resolver o problema dos outliers utilizando o método Tukey ou Boxplot onde iremos definir os limites inferior e superior a partir do interquartil (IQR) e dos primeiros (Q1) e terceiros (Q3) quartis.

Quartis são separatrizes que dividem um conjunto de dados em 4 partes iguais. O objetivo das separatrizes é proporcionar uma melhor ideia da dispersão do dataset, principalmente da simetria ou assimetria da distribuição.

O limite inferior é definido pelo primeiro quartil menos o produto entre o valor 1.5 e o interquartil.

Linf = Q1 – (1.5 * IQR)

O limite superior é definido pelo terceiro quartil mais o produto entre o valor 1.5 e o interquartil.

Lsup = Q3 + (1.5 * IQR)

Em seguida vamos observar se os outliers foram removidos através do boxplot.

Esta função serve para substituir os outliers, onde valores acima do limite superior são substituídos pelo próprio limite superior e valores abaixo do limite inferior são substituídos pelo próprio limite inferior.

Observando o boxplot novamente, percebemos que não existem mais outliers.

Observando as variáveis depois de separadas.

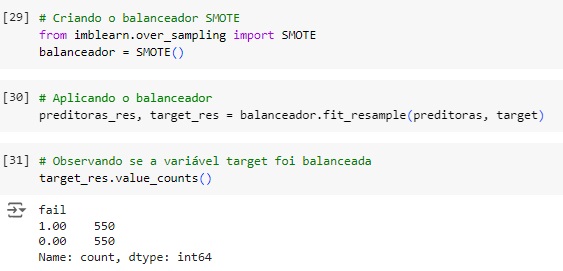
Agora vamos balancear os dados com o SMOTE(), o comando vai avaliar o banco de dados e vai criar novos dados para igualar as variáveis target. Em seguida vamos aplicar o balanceador, vamos criar duas novas variáveis preditoras_res e target_res que serão os resultados do balanceamento em seguida usaremos o fit_resmple() que é o método balanceardor do SMOTE(), e passamos os parâmetros que queremos balancear, no caso preditoras e target

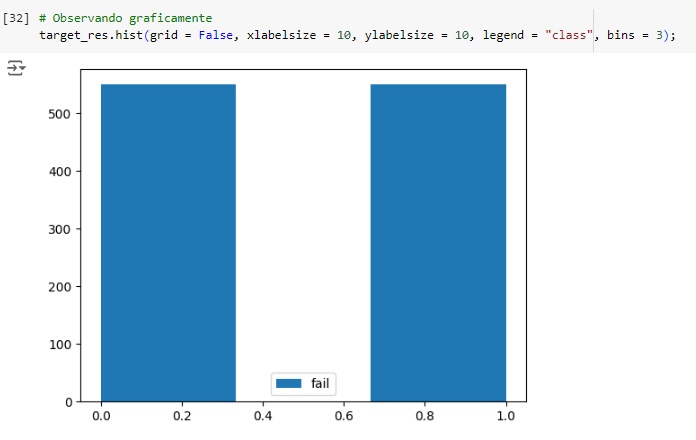
Visualizando através do gráfico, percebemos que a variável target foi balanceada corretamente.

Usando o train_test_split() vamos dividir a base de dados em treino e teste, sendo 80% dos dados para treinamento e 20% para teste.

Em seguida vamos padronizar os dados das variáveis preditoras para colocá-los na mesma escala, vamos utilizar o StandardScaler() e o fit_transform() para isso.

Agora vamos inicializar os modelos de machine learning que vamos testar, Random Forest, Gradient Boosting, Logistic Regression e SVM. Vamos treinar com cada um destes modelos e vamos fazer a avaliação com o que apresentar a melhor acurácia.

Agora vamos encontrar o melhor modelo preditivo que foram definidos acima, utilizando a técnica de Grid Search para otimização de hiperparâmetros. Vamos explicar detalhadamente o que cada parte faz:

best_models: é um dicionário que armazenará o melhor estimador para cada modelo.

best_accuracy: é a maior acurácia obtida dentre todos os modelos testados.

best_model_name: é o nome do modelo que obteve a melhor acurácia.

best_model: é o próprio modelo (estimador) que obteve a melhor acurácia.

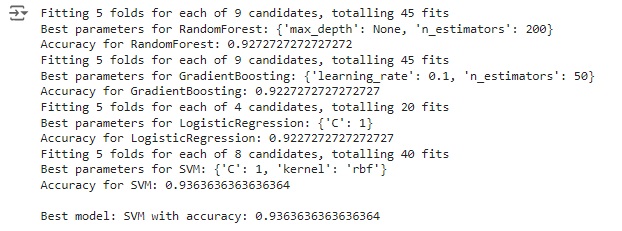
No loop for temos cada modelo em ‘modelos’, um GridSearchCV() é configurado com o modelo atual e seus hiperparâmetros em ‘params’.

GridSearchCV() é treinado usando os dados de treino padronizados (x_treino_padronizado e e y_treino).

O melhor estimador encontrado pelo GridSearchCV() é armazenado em ‘best_models’ com o nome do modelo como chave. Os melhores hiperparâmetros encontrados são impressos, então o modelo será usado para fazer previsões nos dados de teste (x_teste_padronizado), então a acurácia das previsões é calculada e impressa. Se a acurácia deste modelo é a maior até agora, ‘best_accuracy’, ‘best_model_name’ e ‘best_model’ são atualizados. Em eguida o modelo com a melhor acurácia será impresso.

Podemos ver que o modelo de SVM teve a melhor acurácia 93.6%.

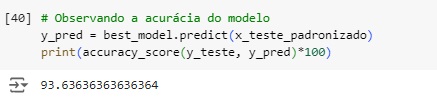
Comparando ‘y_pred’ que é a variável com as previsões com os dados originais ‘y_teste’ podemos perceber que o algoritmo acertou os 7 primeiro valores…

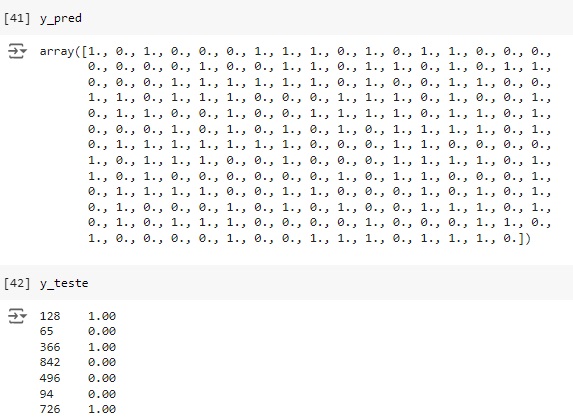
Através do classification report percebemos que o algoritmo consegue identificar corretamente 92% das máquinas que não tem falhas (recall 0.92) e quando identifica um item desta classe a precisão é de 95% (precision 0.95). Para as máquinas que apresentam falha o resultado do algoritmo foi de 95% das identificações corretas (recall 0.95) com 92% de certeza (precision 0.92).

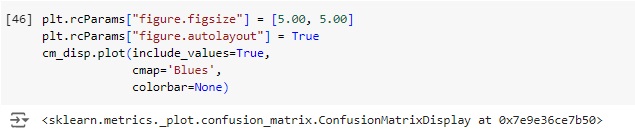
Vamos afazer uma análise a partir da matriz de confusão.

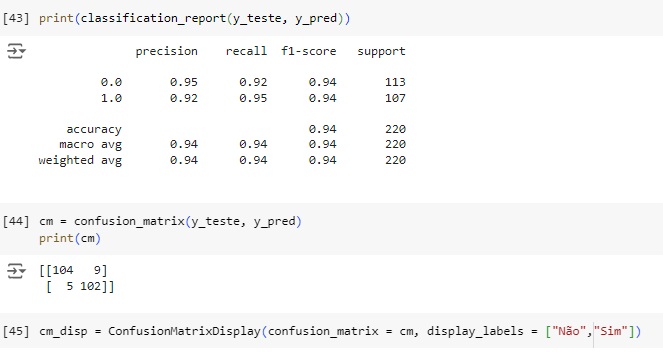
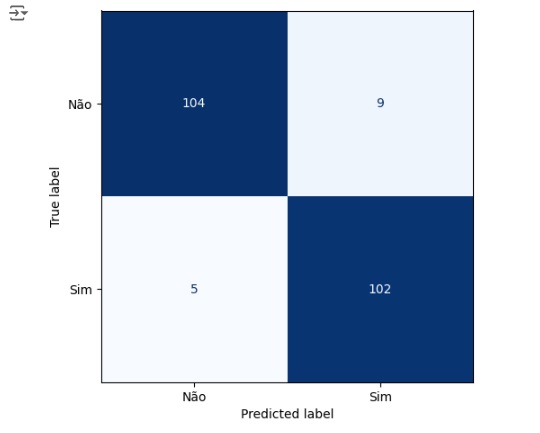
Plotando a matriz de confusão podemos perceber que 104 máquinas não possuem falhas no banco de dados real e foi também o valor que o modelo previu, ou seja, é um verdadeiro positivo. No outro lado da matriz percebemos que segundo os dados reais 102 máquinas tem algum tipo de falha, o mesmo valor que o modelo previu. Com isso conseguimos perceber que a diagonal que está azul mais escuro são os acertos do modelo.

Passando para a diagonal azul claro, percebemos que o banco de dados real tem 9 máquinas sem falha, mas o modelo previu que tem, no caso o modelo errou a previsão. Na outra diagonal percebemos que tem 5 máquinas têm falhas segundo o banco de dados real, mas o modelo previu que não possuem.